Question Number 142945 by Rankut last updated on 07/Jun/21
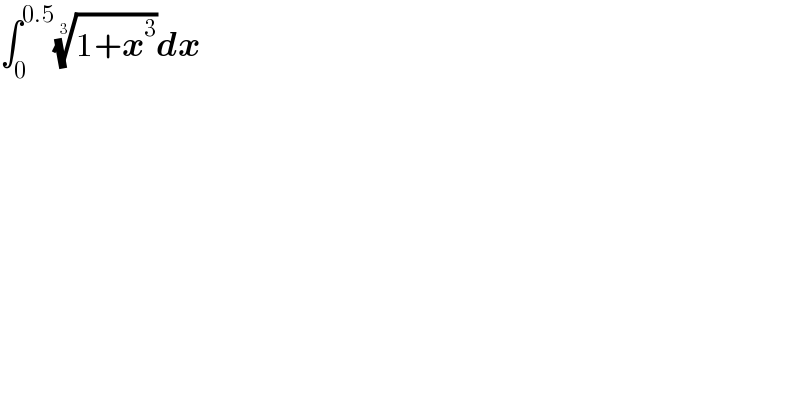
$$\int_{\mathrm{0}} ^{\mathrm{0}.\mathrm{5}} \sqrt[{\mathrm{3}}]{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{3}} }\boldsymbol{{dx}} \\ $$$$ \\ $$
Answered by mindispower last updated on 07/Jun/21
![(1+y)^a =1+Σ_(n≥1) ((Π_(k=0) ^(n−1) (a−k))/(n!))x^n (1+x^3 )^(1/3) =1+Σ_(n≥1) ((Π_(k=0) ^(n−1) (−1)^n (k−(1/3)))/(n!))x^n =(1/2)(1+Σ_(n≥1) (((k−(1/3))_n .n!)/((n+1)!)).(((((−1)/2))^n )/(n!))) =(1/2) _2 F_1 (−(1/3),1;2;[−(1/2)])](https://www.tinkutara.com/question/Q142946.png)
$$\left(\mathrm{1}+{y}\right)^{{a}} =\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({a}−{k}\right)}{{n}!}{x}^{{n}} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} =\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left(−\mathrm{1}\right)^{{n}} \left({k}−\frac{\mathrm{1}}{\mathrm{3}}\right)}{{n}!}{x}^{{n}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left({k}−\frac{\mathrm{1}}{\mathrm{3}}\right)_{{n}} .{n}!}{\left({n}+\mathrm{1}\right)!}.\frac{\left(\frac{−\mathrm{1}}{\mathrm{2}}\right)^{{n}} }{{n}!}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(−\frac{\mathrm{1}}{\mathrm{3}},\mathrm{1};\mathrm{2};\left[−\frac{\mathrm{1}}{\mathrm{2}}\right]\right) \\ $$$$ \\ $$
