Question Number 137969 by rs4089 last updated on 08/Apr/21
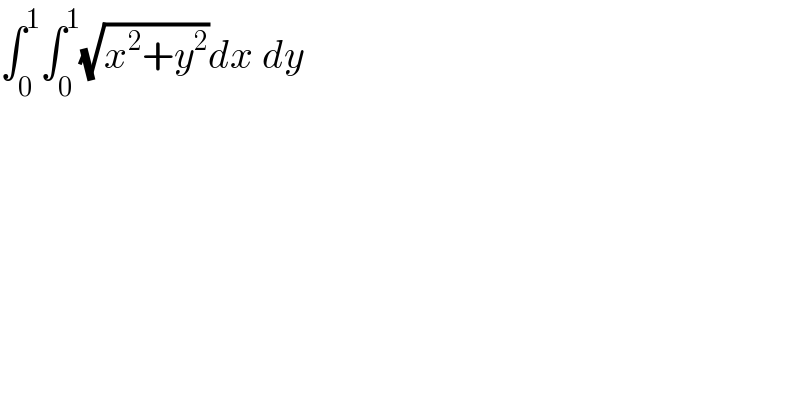
$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }{dx}\:{dy} \\ $$
Answered by EnterUsername last updated on 08/Apr/21
![{ ((x=rcosθ)),((y=rsinθ)) :} ∫_0 ^1 ∫_0 ^1 (√(x^2 +y^2 ))dxdy=∫_0 ^(π/2) ∫_0 ^(√2) r^2 drdθ =(π/2)[(r^3 /3)]_0 ^(√2) =((√2)/3)π](https://www.tinkutara.com/question/Q137972.png)
$$\begin{cases}{\mathrm{x}=\mathrm{rcos}\theta}\\{\mathrm{y}=\mathrm{rsin}\theta}\end{cases} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} }\mathrm{dxdy}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \mathrm{r}^{\mathrm{2}} \mathrm{drd}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\left[\frac{\mathrm{r}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} =\frac{\sqrt{\mathrm{2}}}{\mathrm{3}}\pi \\ $$
