Menu Close

0-1-1-4x-2-dx-

Tinku Tara
Pin




Question Number 65736 by malwaan last updated on 03/Aug/19
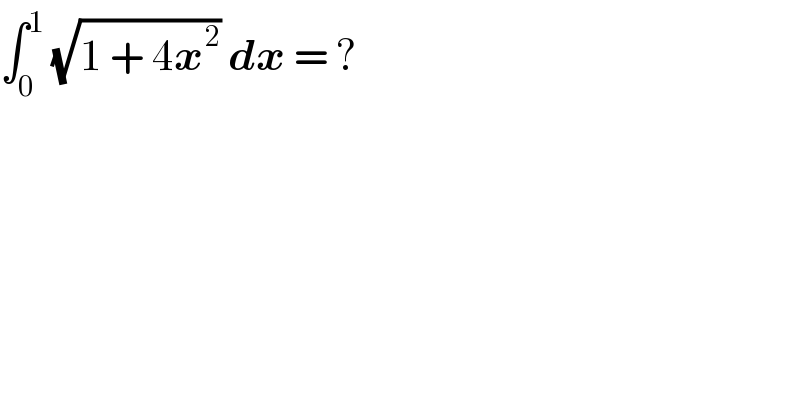
∫_0 ^1 (√(1 + 4x^2 )) dx = ?
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{1}\:+\:\mathrm{4}\boldsymbol{{x}}^{\mathrm{2}} }\:\boldsymbol{{dx}}\:=\:? \\ $$
Commented by Souvik Ghosh last updated on 03/Aug/19
let u=2x⇔du=2dx ∫_0 ^2 (√((1+u^2 ))) du/2 ⇒(1/2)[((u(√(1+u^2 )))/2) +(1/2)ln {u+(√(1+u^2 ))}]_0 ^2 ⇒(1/2)[(√5)+(1/2)ln (2+(√5))]
$${let}\:\:\:{u}=\mathrm{2}{x}\Leftrightarrow{du}=\mathrm{2}{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \sqrt{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:{du}/\mathrm{2} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{{u}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left\{{u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right\}\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\left[\sqrt{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\right] \\ $$
Commented by mathmax by abdo last updated on 03/Aug/19
changement 2x =sh(t) give t =argsh(2x) =ln(2x+(√(1+4x^2 ))) ∫_0 ^1 (√(1+4x^2 ))dx =∫_0 ^(ln(2+(√5))) (√(1+sh^2 t))((ch(t))/2)dt =(1/2) ∫_0 ^(ln(2+(√5))) ch^2 t dt =(1/4) ∫_0 ^(ln(2+(√5))) (1+ch(2t))dt =((ln(2+(√5)))/4) +(1/8)[sh(2t)]_0 ^(ln(2+(√5))) =((ln(2+(√5)))/4) +(1/8)[((e^(2t) −e^(−2t) )/2)]_0 ^(ln(2+(√5))) =((ln(2+(√5)))/4) +(1/(16)){(2+(√5))^2 −(1/((2+(√5))^2 ))}
$${changement}\:\mathrm{2}{x}\:={sh}\left({t}\right)\:{give}\:{t}\:={argsh}\left(\mathrm{2}{x}\right)\:={ln}\left(\mathrm{2}{x}+\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}\:=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} \sqrt{\mathrm{1}+{sh}^{\mathrm{2}} {t}}\frac{{ch}\left({t}\right)}{\mathrm{2}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} {ch}^{\mathrm{2}} {t}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} \left(\mathrm{1}+{ch}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$=\frac{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[{sh}\left(\mathrm{2}{t}\right)\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[\frac{{e}^{\mathrm{2}{t}} −{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)} \\ $$$$=\frac{{ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{16}}\left\{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }\right\} \\ $$
Answered by MJS last updated on 03/Aug/19
∫(√(1+4x^2 ))dx= [t=arcsinh 2x → dx=((√(1+4x^2 ))/2)dt] =(1/2)∫cosh^2 t dt=(1/4)t+(1/4)sinh 2t = =(1/4)arcsinh 2x +((x(√(1+4x^2 )))/2) +C ∫_0 ^1 (√(1+4x^2 ))dx=(1/4)arcsinh 2 +((√5)/2) (=(1/4)ln (2+(√5)) +((√5)/2))
$$\int\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsinh}\:\mathrm{2}{x}\:\rightarrow\:{dx}=\frac{\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{cosh}^{\mathrm{2}} \:{t}\:{dt}=\frac{\mathrm{1}}{\mathrm{4}}{t}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sinh}\:\mathrm{2}{t}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{arcsinh}\:\mathrm{2}{x}\:+\frac{{x}\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }}{\mathrm{2}}\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}+\mathrm{4}{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{arcsinh}\:\mathrm{2}\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\left(=\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\:+\frac{\sqrt{\mathrm{5}}}{\mathrm{2}}\right) \\ $$

Pin