Question Number 135366 by Dwaipayan Shikari last updated on 12/Mar/21
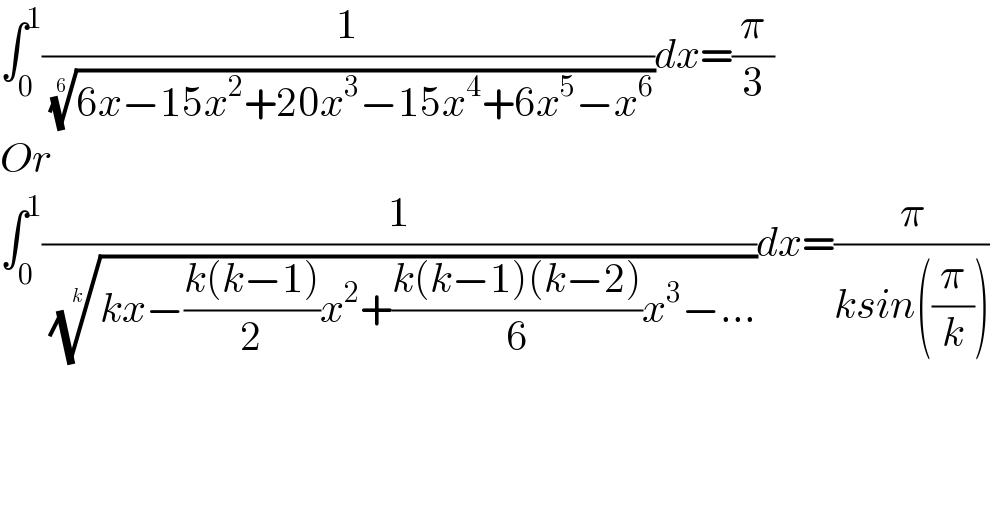
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}}]{\mathrm{6}{x}−\mathrm{15}{x}^{\mathrm{2}} +\mathrm{20}{x}^{\mathrm{3}} −\mathrm{15}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{5}} −{x}^{\mathrm{6}} }}{dx}=\frac{\pi}{\mathrm{3}} \\ $$$${Or} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\:\sqrt[{{k}}]{{kx}−\frac{{k}\left({k}−\mathrm{1}\right)}{\mathrm{2}}{x}^{\mathrm{2}} +\frac{{k}\left({k}−\mathrm{1}\right)\left({k}−\mathrm{2}\right)}{\mathrm{6}}{x}^{\mathrm{3}} −…}}{dx}=\frac{\pi}{{ksin}\left(\frac{\pi}{{k}}\right)} \\ $$
Answered by Olaf last updated on 12/Mar/21
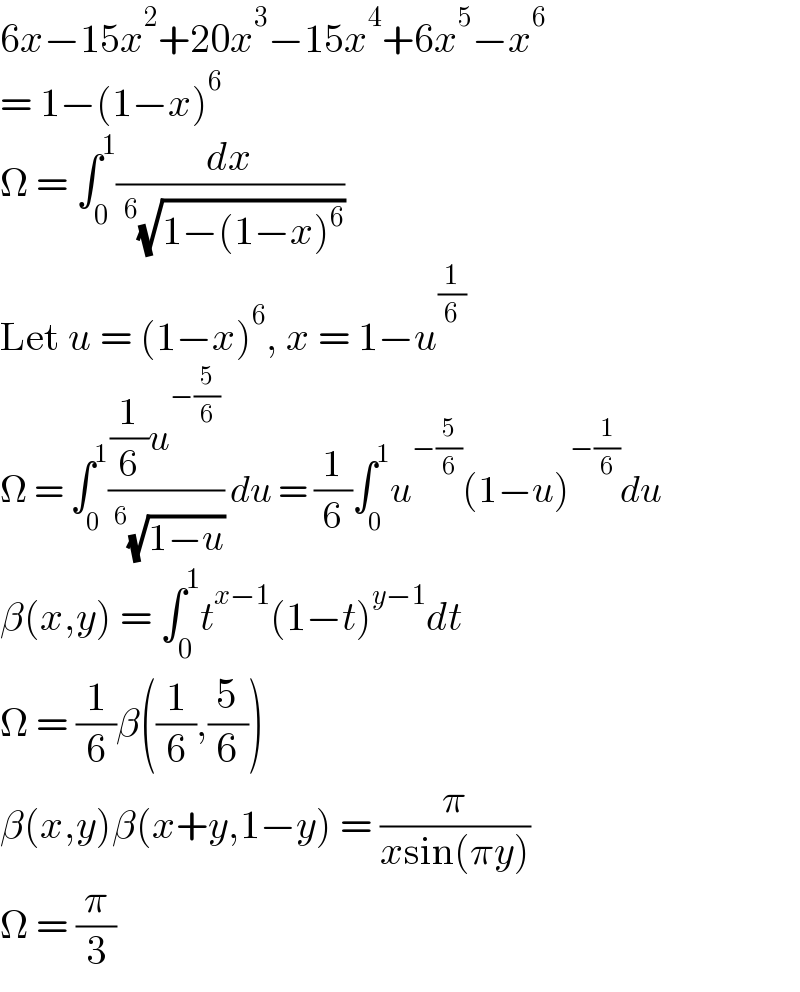
$$\mathrm{6}{x}−\mathrm{15}{x}^{\mathrm{2}} +\mathrm{20}{x}^{\mathrm{3}} −\mathrm{15}{x}^{\mathrm{4}} +\mathrm{6}{x}^{\mathrm{5}} −{x}^{\mathrm{6}} \\ $$$$=\:\mathrm{1}−\left(\mathrm{1}−{x}\right)^{\mathrm{6}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:^{\mathrm{6}} \sqrt{\mathrm{1}−\left(\mathrm{1}−{x}\right)^{\mathrm{6}} }} \\ $$$$\mathrm{Let}\:{u}\:=\:\left(\mathrm{1}−{x}\right)^{\mathrm{6}} ,\:{x}\:=\:\mathrm{1}−{u}^{\frac{\mathrm{1}}{\mathrm{6}}} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\frac{\mathrm{1}}{\mathrm{6}}{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} }{\:^{\mathrm{6}} \sqrt{\mathrm{1}−{u}}}\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{5}}{\mathrm{6}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{6}}} {du} \\ $$$$\beta\left({x},{y}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{x}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{{y}−\mathrm{1}} {dt} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{6}}\beta\left(\frac{\mathrm{1}}{\mathrm{6}},\frac{\mathrm{5}}{\mathrm{6}}\right) \\ $$$$\beta\left({x},{y}\right)\beta\left({x}+{y},\mathrm{1}−{y}\right)\:=\:\frac{\pi}{{x}\mathrm{sin}\left(\pi{y}\right)} \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{3}} \\ $$
