Question Number 141947 by mnjuly1970 last updated on 25/May/21
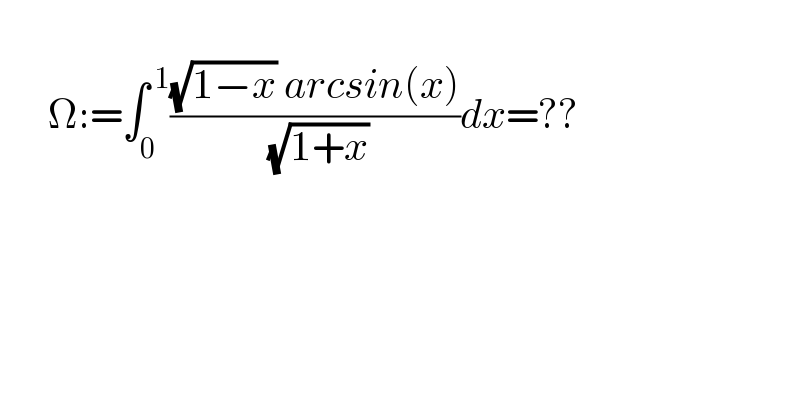
$$ \\ $$$$\:\:\:\:\:\:\Omega:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{\mathrm{1}−{x}}\:{arcsin}\left({x}\right)}{\:\sqrt{\mathrm{1}+{x}}}{dx}=?? \\ $$
Answered by qaz last updated on 25/May/21

$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−\mathrm{x}}\mathrm{sin}^{−\mathrm{1}} \mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}\right)\mathrm{sin}^{−\mathrm{1}} \mathrm{x}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\mathrm{1}−\mathrm{sin}\:\mathrm{u}\right)\mathrm{udu} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{udu}−\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{usin}\:\mathrm{udu} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\pi^{\mathrm{2}} +\mathrm{ucos}\:\mathrm{u}\mid_{\mathrm{0}} ^{\pi/\mathrm{2}} −\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \mathrm{cos}\:\mathrm{udu} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\pi^{\mathrm{2}} −\mathrm{1} \\ $$
Commented by mnjuly1970 last updated on 25/May/21
$$\:\:\:{thanks}\:{alot}\:{mr}\:{qaz}.. \\ $$
Answered by mathmax by abdo last updated on 25/May/21
![Φ=∫_0 ^1 (((√(1−x))arcsin(x))/( (√(1+x))))dx ⇒Φ=∫_0 ^1 (((√(1−x^2 ))arcsinx)/(1+x))dx =_(x=sint) ∫_0 ^(π/2) ((tcost)/(1+sint)) cost dt =∫_0 ^(π/2) ((t(1−sin^2 t))/(1+sint))dt =∫_0 ^(π/2) t(1−sint)dt =∫_0 ^(π/2) t dt−∫_0 ^(π/2) tsint dt we have ∫_0 ^(π/2) tdt =[(t^2 /2)]_0 ^(π/2) =(π^2 /8) ∫_0 ^(π/2) tsint dt =[−tcost]_0 ^(π/2) +∫_0 ^(π/2) cost dt =0+1=1 ⇒ Φ=(π^2 /8)−1★](https://www.tinkutara.com/question/Q141985.png)
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\mathrm{x}}\mathrm{arcsin}\left(\mathrm{x}\right)}{\:\sqrt{\mathrm{1}+\mathrm{x}}}\mathrm{dx}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{arcsinx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$$$=_{\mathrm{x}=\mathrm{sint}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{tcost}}{\mathrm{1}+\mathrm{sint}}\:\mathrm{cost}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{t}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{t}\right)}{\mathrm{1}+\mathrm{sint}}\mathrm{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{t}\left(\mathrm{1}−\mathrm{sint}\right)\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{t}\:\mathrm{dt}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tsint}\:\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{tdt}\:=\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{tsint}\:\mathrm{dt}\:=\left[−\mathrm{tcost}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cost}\:\mathrm{dt}\:=\mathrm{0}+\mathrm{1}=\mathrm{1}\:\Rightarrow \\ $$$$\Phi=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}−\mathrm{1}\bigstar \\ $$$$ \\ $$
