Menu Close

0-1-1-x-x-2-x-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 66740 by behi83417@gmail.com last updated on 19/Aug/19
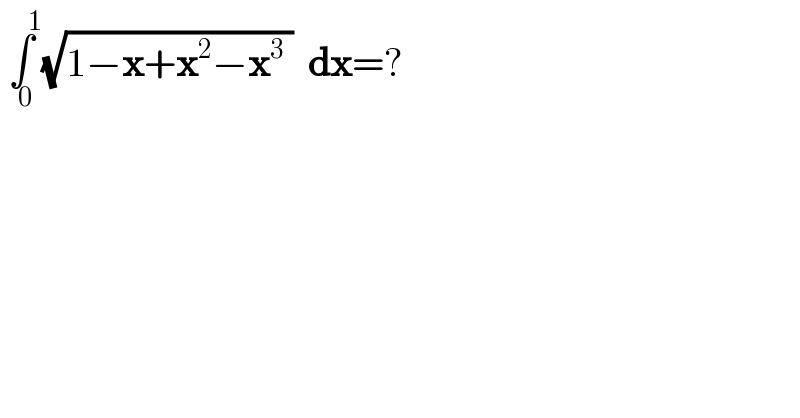
∫_( 0) ^( 1) (√(1−x+x^2 −x^3 )) dx=?
$$\underset{\:\:\mathrm{0}} {\overset{\:\:\:\:\:\:\:\mathrm{1}} {\int}}\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} −\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:}\:\:\boldsymbol{\mathrm{dx}}=? \\ $$
Commented by mathmax by abdo last updated on 21/Aug/19
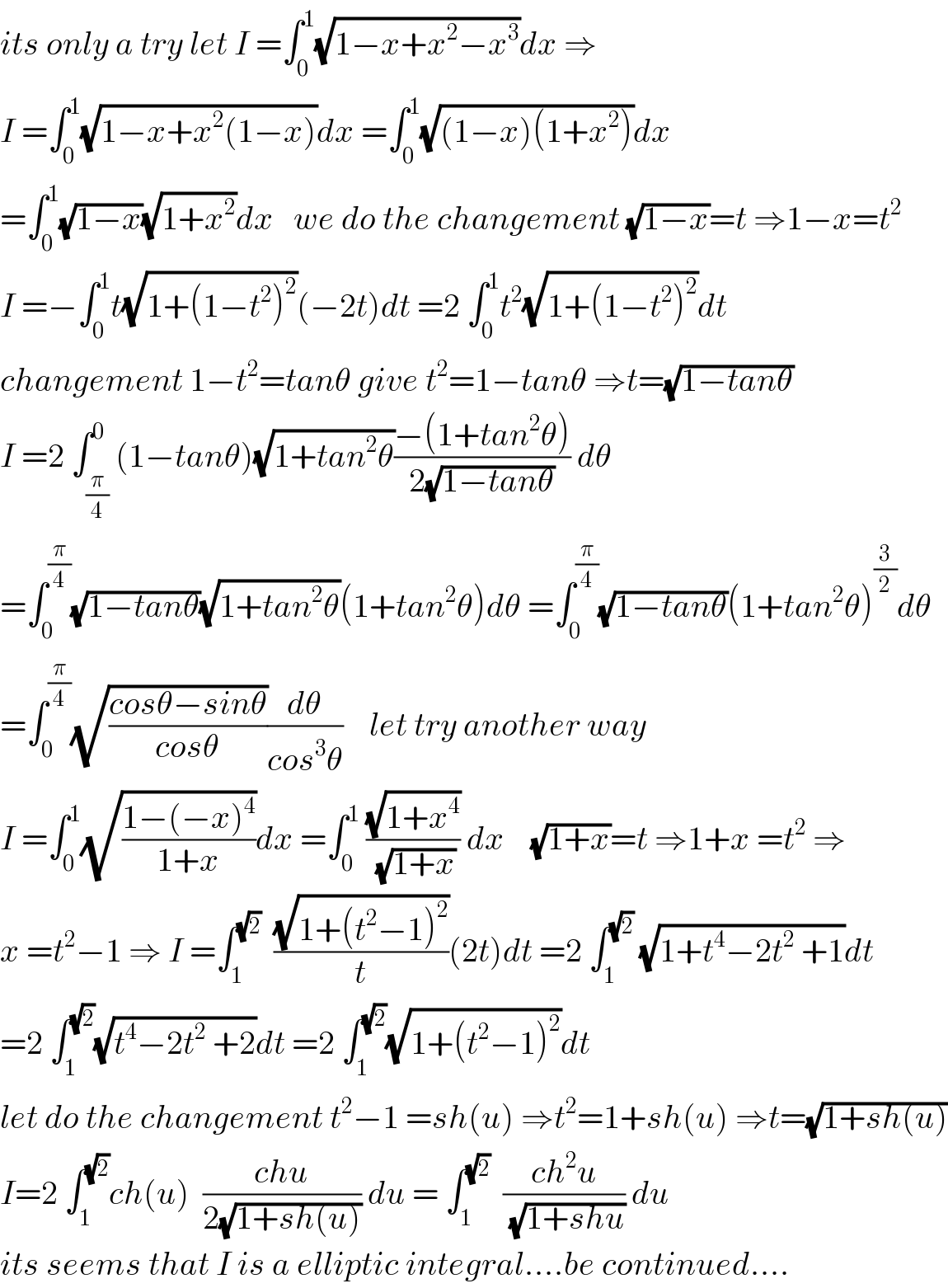
its only a try let I =∫_0 ^1 (√(1−x+x^2 −x^3 ))dx ⇒ I =∫_0 ^1 (√(1−x+x^2 (1−x)))dx =∫_0 ^1 (√((1−x)(1+x^2 )))dx =∫_0 ^1 (√(1−x))(√(1+x^2 ))dx we do the changement (√(1−x))=t ⇒1−x=t^2 I =−∫_0 ^1 t(√(1+(1−t^2 )^2 ))(−2t)dt =2 ∫_0 ^1 t^2 (√(1+(1−t^2 )^2 ))dt changement 1−t^2 =tanθ give t^2 =1−tanθ ⇒t=(√(1−tanθ)) I =2 ∫_(π/4) ^0 (1−tanθ)(√(1+tan^2 θ))((−(1+tan^2 θ))/(2(√(1−tanθ)))) dθ =∫_0 ^(π/4) (√(1−tanθ))(√(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/4) (√(1−tanθ))(1+tan^2 θ)^(3/2) dθ =∫_0 ^(π/4) (√((cosθ−sinθ)/(cosθ)))(dθ/(cos^3 θ)) let try another way I =∫_0 ^1 (√((1−(−x)^4 )/(1+x)))dx =∫_0 ^1 ((√(1+x^4 ))/( (√(1+x)))) dx (√(1+x))=t ⇒1+x =t^2 ⇒ x =t^2 −1 ⇒ I =∫_1 ^(√2) ((√(1+(t^2 −1)^2 ))/t)(2t)dt =2 ∫_1 ^(√2) (√(1+t^4 −2t^2 +1))dt =2 ∫_1 ^(√2) (√(t^4 −2t^2 +2))dt =2 ∫_1 ^(√2) (√(1+(t^2 −1)^2 ))dt let do the changement t^2 −1 =sh(u) ⇒t^2 =1+sh(u) ⇒t=(√(1+sh(u))) I=2 ∫_1 ^(√2) ch(u) ((chu)/(2(√(1+sh(u))))) du = ∫_1 ^(√2) ((ch^2 u)/( (√(1+shu)))) du its seems that I is a elliptic integral....be continued....
$${its}\:{only}\:{a}\:{try}\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }{dx}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}+{x}^{\mathrm{2}} \left(\mathrm{1}−{x}\right)}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\mathrm{1}−{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:\:{we}\:{do}\:{the}\:{changement}\:\sqrt{\mathrm{1}−{x}}={t}\:\Rightarrow\mathrm{1}−{x}={t}^{\mathrm{2}} \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} {t}\sqrt{\mathrm{1}+\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\left(−\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \sqrt{\mathrm{1}+\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt} \\ $$$${changement}\:\mathrm{1}−{t}^{\mathrm{2}} ={tan}\theta\:{give}\:{t}^{\mathrm{2}} =\mathrm{1}−{tan}\theta\:\Rightarrow{t}=\sqrt{\mathrm{1}−{tan}\theta} \\ $$$${I}\:=\mathrm{2}\:\int_{\frac{\pi}{\mathrm{4}}} ^{\mathrm{0}} \left(\mathrm{1}−{tan}\theta\right)\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\frac{−\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)}{\mathrm{2}\sqrt{\mathrm{1}−{tan}\theta}}\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}−{tan}\theta}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\mathrm{1}−{tan}\theta}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \sqrt{\frac{{cos}\theta−{sin}\theta}{{cos}\theta}}\frac{{d}\theta}{{cos}^{\mathrm{3}} \theta}\:\:\:\:{let}\:{try}\:{another}\:{way} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}−\left(−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}{\:\sqrt{\mathrm{1}+{x}}}\:{dx}\:\:\:\:\sqrt{\mathrm{1}+{x}}={t}\:\Rightarrow\mathrm{1}+{x}\:={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}\:={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow\:{I}\:=\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{\sqrt{\mathrm{1}+\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }}{{t}}\left(\mathrm{2}{t}\right){dt}\:=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}}{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \sqrt{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{2}}{dt}\:=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \sqrt{\mathrm{1}+\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{dt} \\ $$$${let}\:{do}\:{the}\:{changement}\:{t}^{\mathrm{2}} −\mathrm{1}\:={sh}\left({u}\right)\:\Rightarrow{t}^{\mathrm{2}} =\mathrm{1}+{sh}\left({u}\right)\:\Rightarrow{t}=\sqrt{\mathrm{1}+{sh}\left({u}\right)} \\ $$$${I}=\mathrm{2}\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} {ch}\left({u}\right)\:\:\frac{{chu}}{\mathrm{2}\sqrt{\mathrm{1}+{sh}\left({u}\right)}}\:{du}\:=\:\int_{\mathrm{1}} ^{\sqrt{\mathrm{2}}} \:\:\frac{{ch}^{\mathrm{2}} {u}}{\:\sqrt{\mathrm{1}+{shu}}}\:{du} \\ $$$${its}\:{seems}\:{that}\:{I}\:{is}\:{a}\:{elliptic}\:{integral}….{be}\:{continued}…. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *