0-1-3-3x-1-5-dx- – Tinku Tara

Question Number 65593 by Rio Michael last updated on 31/Jul/19

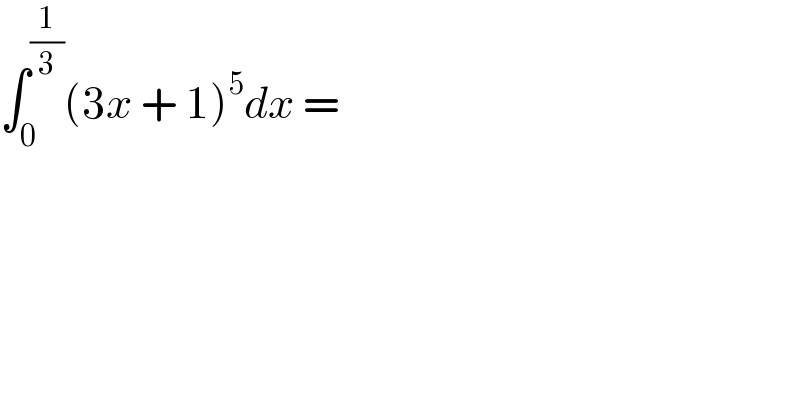
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{3}{x}\:+\:\mathrm{1}\right)^{\mathrm{5}} {dx}\:= \\ $$

Commented by mathmax by abdo last updated on 31/Jul/19

let I =∫_0 ^(1/3) (3x+1)^5 changement 3x+1 =t give I =∫_1 ^2 t^5 (dt/3) =(1/3)[(t^6 /6)]_1 ^2 =(1/3){(2^6 /6)−(1/6)} =(2^6 /(3×6))−(1/(18)) =(2^5 /9)−(1/(18)) =...

$${let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{5}} \:\:{changement}\:\:\mathrm{3}{x}+\mathrm{1}\:={t}\:{give} \\ $$$${I}\:=\int_{\mathrm{1}} ^{\mathrm{2}} {t}^{\mathrm{5}} \:\frac{{dt}}{\mathrm{3}}\:=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{{t}^{\mathrm{6}} }{\mathrm{6}}\right]_{\mathrm{1}} ^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{3}}\left\{\frac{\mathrm{2}^{\mathrm{6}} }{\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{6}}\right\}\:=\frac{\mathrm{2}^{\mathrm{6}} }{\mathrm{3}×\mathrm{6}}−\frac{\mathrm{1}}{\mathrm{18}}\:=\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{9}}−\frac{\mathrm{1}}{\mathrm{18}}\:=… \\ $$

Commented by Rio Michael last updated on 31/Jul/19

$${thanks} \\ $$

Commented by Rio Michael last updated on 31/Jul/19

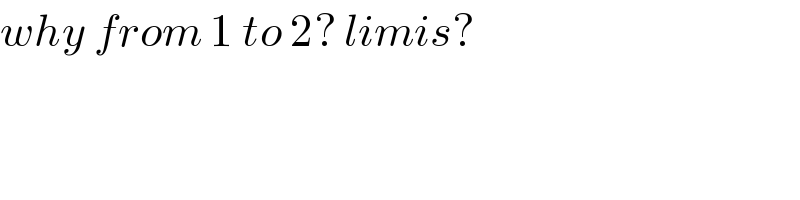
$${why}\:{from}\:\mathrm{1}\:{to}\:\mathrm{2}?\:{limis}? \\ $$

Commented by mathmax by abdo last updated on 01/Aug/19

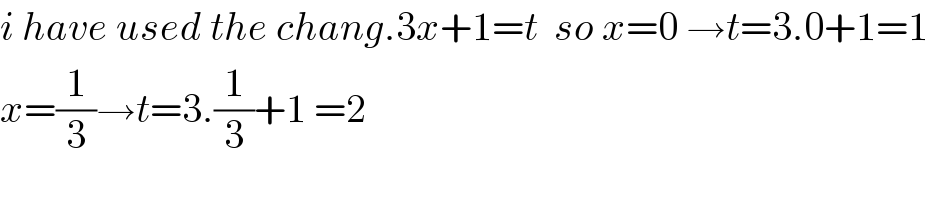
i have used the chang.3x+1=t so x=0 →t=3.0+1=1 x=(1/3)→t=3.(1/3)+1 =2

$${i}\:{have}\:{used}\:{the}\:{chang}.\mathrm{3}{x}+\mathrm{1}={t}\:\:{so}\:{x}=\mathrm{0}\:\rightarrow{t}=\mathrm{3}.\mathrm{0}+\mathrm{1}=\mathrm{1} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\rightarrow{t}=\mathrm{3}.\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\:=\mathrm{2} \\ $$

Commented by Rio Michael last updated on 01/Aug/19

$${thank}\:{you}\:{sir} \\ $$

Answered by AnjanDey last updated on 31/Jul/19

Let,3x+1=z or,3dx=dz or,dx=(dz/3) ∴∫_0 ^(1/3) z^5 ∙(dz/3) =(1/3)∫_0 ^(1/3) z^5 dz =(1/3)[(z^6 /6)]_0 ^(1/3) =(1/3)[(((3x+1)^6 )/6)]_0 ^(1/3) =(1/3)×(1/6)[(3x+1)^6 ]_0 ^(1/3) =(1/(18))[(3×(1/3)+1)^6 −(3×0+1)^6 ] =(1/(18))[2^6 −1^6 ] =(1/(18))[64−1] =(1/(18))×63 =(7/2)

$$\mathrm{Let},\mathrm{3}{x}+\mathrm{1}=\mathrm{z}\: \\ $$$$\:\:\:\:\:\mathrm{or},\mathrm{3}{dx}={d}\mathrm{z} \\ $$$$\:\:\:\:\:\mathrm{or},{dx}=\frac{{d}\mathrm{z}}{\mathrm{3}} \\ $$$$\therefore\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{z}^{\mathrm{5}} \centerdot\frac{{d}\mathrm{z}}{\mathrm{3}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \mathrm{z}^{\mathrm{5}} \:{d}\mathrm{z} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{z}^{\mathrm{6}} }{\mathrm{6}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{6}} }{\mathrm{6}}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{1}}{\mathrm{6}}\left[\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{6}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{18}}\left[\left(\mathrm{3}×\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{6}} −\left(\mathrm{3}×\mathrm{0}+\mathrm{1}\right)^{\mathrm{6}} \right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{18}}\left[\mathrm{2}^{\mathrm{6}} −\mathrm{1}^{\mathrm{6}} \right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{18}}\left[\mathrm{64}−\mathrm{1}\right] \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{18}}×\mathrm{63} \\ $$$$\:\:=\frac{\mathrm{7}}{\mathrm{2}} \\ $$

Commented by Prithwish sen last updated on 01/Aug/19

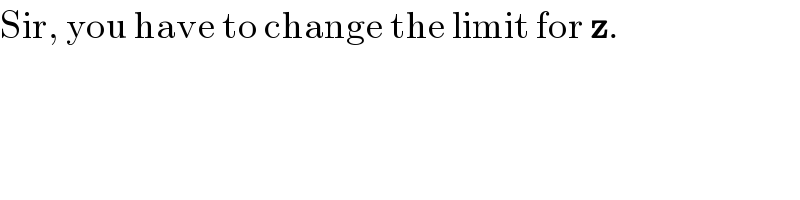
Sir, you have to change the limit for z.

$$\mathrm{Sir},\:\mathrm{you}\:\mathrm{have}\:\mathrm{to}\:\mathrm{change}\:\mathrm{the}\:\mathrm{limit}\:\mathrm{for}\:\boldsymbol{\mathrm{z}}. \\ $$

Facebook Tweet Pin