Question Number 65592 by Rio Michael last updated on 31/Jul/19
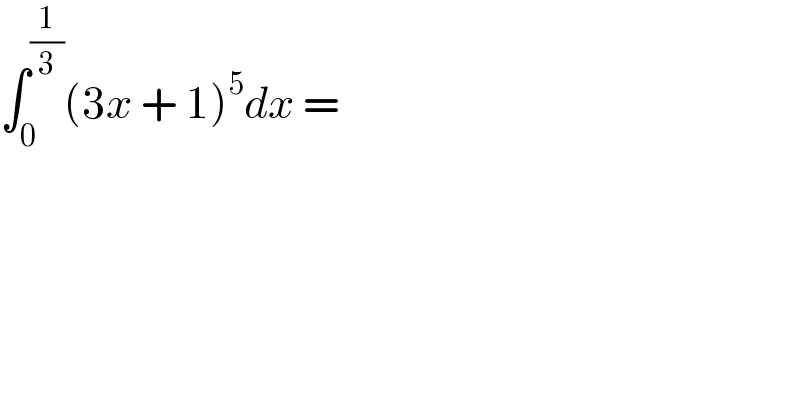
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{3}{x}\:+\:\mathrm{1}\right)^{\mathrm{5}} {dx}\:= \\ $$
Answered by mr W last updated on 31/Jul/19
![∫_0 ^(1/3) (3x + 1)^5 dx =(1/3)∫_0 ^(1/3) (3x + 1)^5 d(3x+1) =(1/(3×6))[(3x+1)^6 ]_0 ^(1/3) =(1/(3×6))[2^6 −1^6 ] =((63)/(3×6)) =(7/2)](https://www.tinkutara.com/question/Q65610.png)
$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{3}{x}\:+\:\mathrm{1}\right)^{\mathrm{5}} {dx}\: \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{3}{x}\:+\:\mathrm{1}\right)^{\mathrm{5}} {d}\left(\mathrm{3}{x}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}×\mathrm{6}}\left[\left(\mathrm{3}{x}+\mathrm{1}\right)^{\mathrm{6}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}×\mathrm{6}}\left[\mathrm{2}^{\mathrm{6}} −\mathrm{1}^{\mathrm{6}} \right] \\ $$$$=\frac{\mathrm{63}}{\mathrm{3}×\mathrm{6}} \\ $$$$=\frac{\mathrm{7}}{\mathrm{2}} \\ $$
