Question Number 4957 by ankit chakravarti last updated on 26/Mar/16
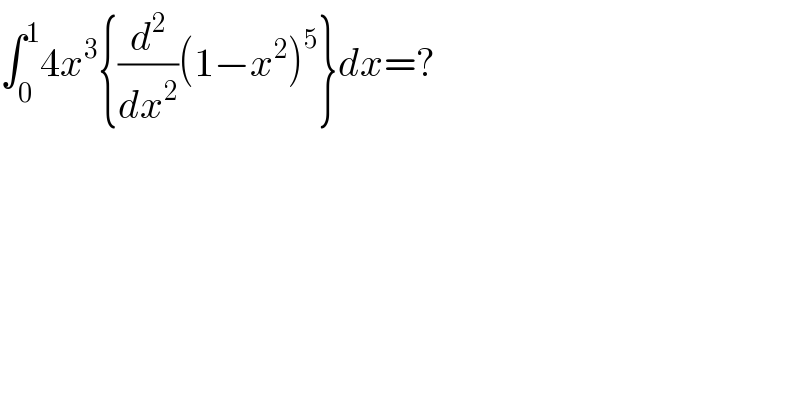
$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left\{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right\}{dx}=? \\ $$
Commented by ankit chakravarti last updated on 26/Mar/16

$${please}\:{solve}….. \\ $$
Answered by Yozzii last updated on 26/Mar/16
![Integrating by parts we obtain I=∫_0 ^1 4x^3 {(d^2 /dx^2 )(1−x^2 )^5 }dx I=4x^3 (d/dx)(1−x^2 )^5 ∣_0 ^1 −∫_0 ^1 12x^2 ((d/dx)(1−x^2 )^5 )dx I=0−12([x^2 (1−x^2 )^5 ]_0 ^1 −∫_0 ^1 2x(1−x^2 )^5 dx) I=(−12)∫_0 ^1 (−2x)(1−x^2 )^5 dx Let u=1−x^2 ⇒du=−2xdx ⇒I=−12∫_1 ^0 u^5 du=12∫_0 ^1 u^5 du=((12)/6)u^6 ∣_0 ^1 =2.](https://www.tinkutara.com/question/Q4960.png)
$${Integrating}\:{by}\:{parts}\:{we}\:{obtain} \\ $$$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{4}{x}^{\mathrm{3}} \left\{\frac{{d}^{\mathrm{2}} }{{dx}^{\mathrm{2}} }\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right\}{dx} \\ $$$${I}=\mathrm{4}{x}^{\mathrm{3}} \frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \mid_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{12}{x}^{\mathrm{2}} \left(\frac{{d}}{{dx}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right){dx} \\ $$$${I}=\mathrm{0}−\mathrm{12}\left(\left[{x}^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{x}\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} {dx}\right) \\ $$$${I}=\left(−\mathrm{12}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{2}{x}\right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} {dx} \\ $$$${Let}\:{u}=\mathrm{1}−{x}^{\mathrm{2}} \Rightarrow{du}=−\mathrm{2}{xdx} \\ $$$$\Rightarrow{I}=−\mathrm{12}\int_{\mathrm{1}} ^{\mathrm{0}} {u}^{\mathrm{5}} {du}=\mathrm{12}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\mathrm{5}} {du}=\frac{\mathrm{12}}{\mathrm{6}}{u}^{\mathrm{6}} \mid_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}. \\ $$$$ \\ $$
