Question Number 143210 by ArielVyny last updated on 11/Jun/21
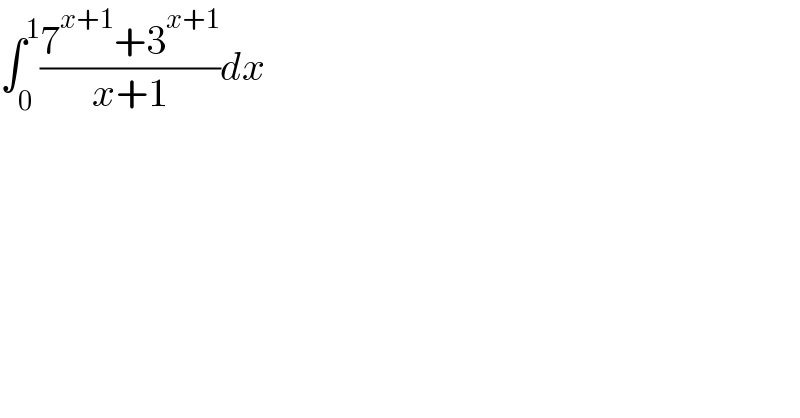
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{7}^{{x}+\mathrm{1}} +\mathrm{3}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}{dx} \\ $$
Answered by MJS_new last updated on 11/Jun/21
![∫((7^(x+1) ++3^(x+1) )/(x+1))dx=∫(7^(x+1) /(x+1))dx+∫(3^(x+1) /(x+1))dx ∫(b^(x+1) /(x+1))dx= [t=(x+1)ln b → dx=(dt/(ln b))] =∫(e^t /t)dt=Ei t =Ei ((x+1)ln b) +C ⇒ answer is ≈17.0130](https://www.tinkutara.com/question/Q143223.png)
$$\int\frac{\mathrm{7}^{{x}+\mathrm{1}} ++\mathrm{3}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}{dx}=\int\frac{\mathrm{7}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}{dx}+\int\frac{\mathrm{3}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}{dx} \\ $$$$ \\ $$$$\int\frac{{b}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\left({x}+\mathrm{1}\right)\mathrm{ln}\:{b}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{ln}\:{b}}\right] \\ $$$$=\int\frac{\mathrm{e}^{{t}} }{{t}}{dt}=\mathrm{Ei}\:{t}\:=\mathrm{Ei}\:\left(\left({x}+\mathrm{1}\right)\mathrm{ln}\:{b}\right)\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\approx\mathrm{17}.\mathrm{0130} \\ $$
