Question Number 131558 by liberty last updated on 06/Feb/21
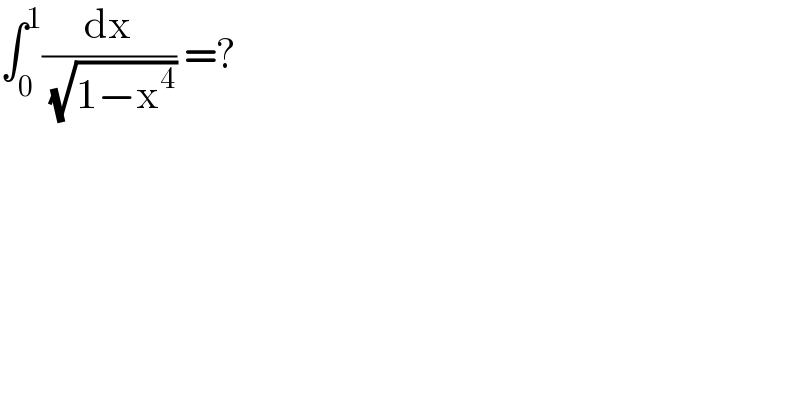
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 06/Feb/21
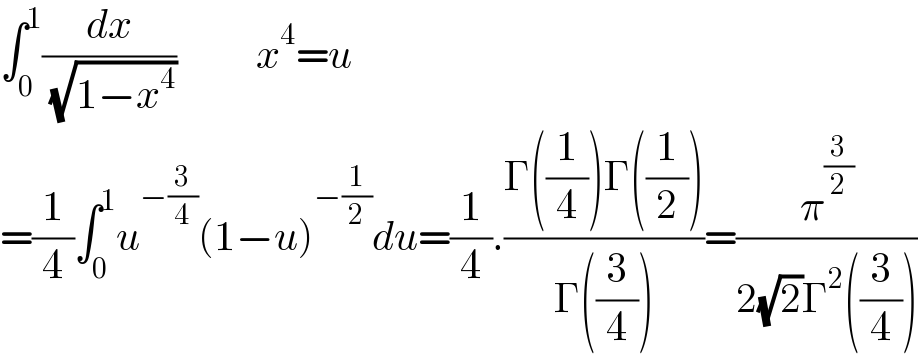
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{4}} ={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−{u}\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {du}=\frac{\mathrm{1}}{\mathrm{4}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{4}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{4}}\right)}=\frac{\pi^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mathrm{2}\sqrt{\mathrm{2}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)} \\ $$
