Question Number 139224 by mnjuly1970 last updated on 24/Apr/21

$$\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)}{{x}}{dx} \\ $$$$\:\:\:\phi=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right)−{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$$\:\:\:\:=\Omega+\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\:\:\:\:\Omega=−\Sigma\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{3}{n}−\mathrm{1}} }{{n}}{dx}=−\underset{{n}=\mathrm{1}\:} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{3}{n}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:=\frac{−\pi^{\mathrm{2}} }{\mathrm{18}}\:…..\succcurlyeq\:\boldsymbol{\phi}=\frac{\pi^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\:\:\:\:\:\:\:…….\frac{\pi^{\mathrm{2}} }{\mathrm{9}}−\frac{\pi^{\mathrm{2}} }{\mathrm{24}}\:=\frac{\mathrm{5}\pi^{\mathrm{2}} }{\mathrm{72}}\: \\ $$
Commented by qaz last updated on 24/Apr/21

$${Great},{Sir},{i}\:{will}\:{complete}\:{that}\:{integral}. \\ $$
Commented by mnjuly1970 last updated on 24/Apr/21
$$\:\:\:{i}\:{appologize}\:.{thank}\:{you}\:{master}… \\ $$
Answered by phanphuoc last updated on 24/Apr/21

$$\pi^{\mathrm{2}} /\mathrm{24}\:??? \\ $$
Answered by mathmax by abdo last updated on 25/Apr/21
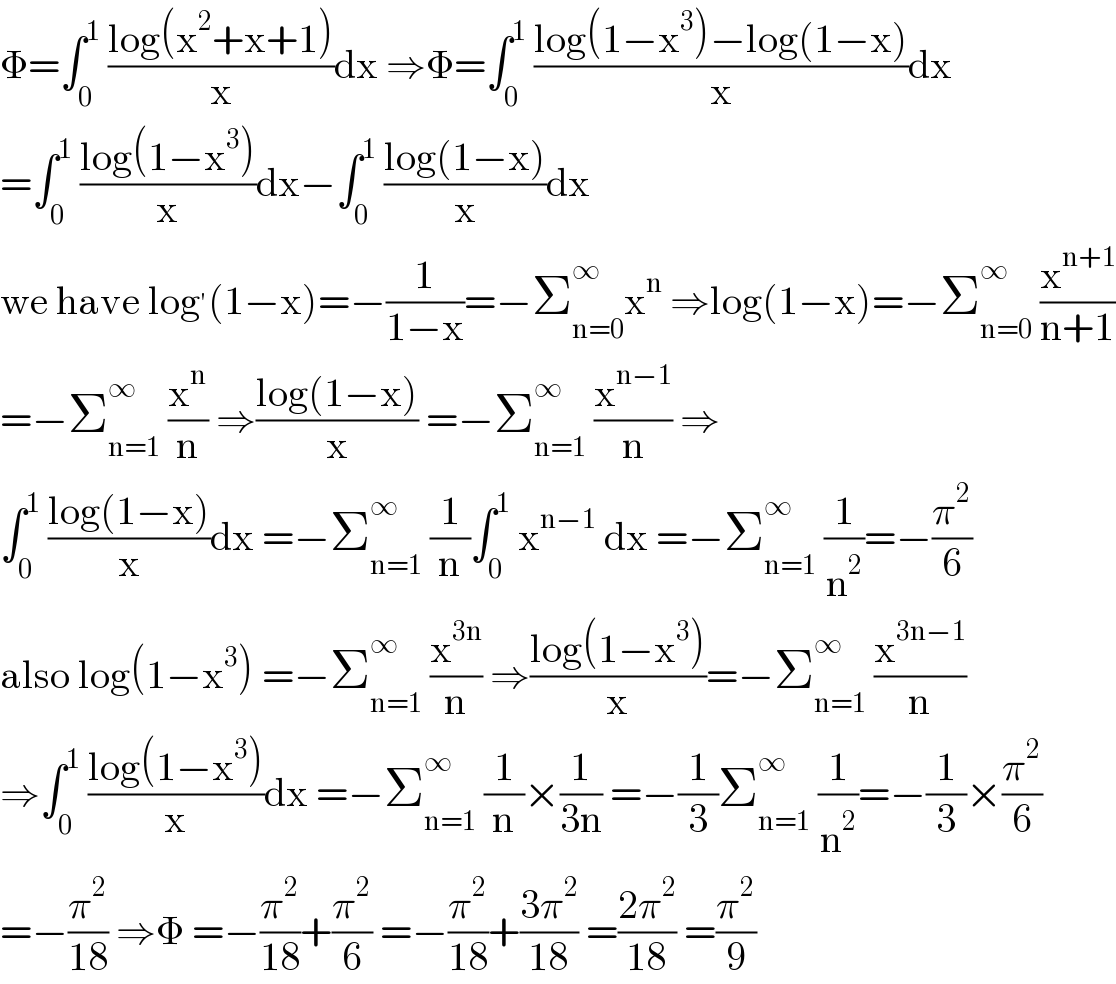
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\mathrm{1}\right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)−\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{log}^{'} \left(\mathrm{1}−\mathrm{x}\right)=−\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{x}^{\mathrm{n}} \:\Rightarrow\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }=−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\mathrm{also}\:\mathrm{log}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{3n}} }{\mathrm{n}}\:\Rightarrow\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}}=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{3n}−\mathrm{1}} }{\mathrm{n}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}\left(\mathrm{1}−\mathrm{x}^{\mathrm{3}} \right)}{\mathrm{x}}\mathrm{dx}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}×\frac{\mathrm{1}}{\mathrm{3n}}\:=−\frac{\mathrm{1}}{\mathrm{3}}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }=−\frac{\mathrm{1}}{\mathrm{3}}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}\:\Rightarrow\Phi\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{18}}+\frac{\mathrm{3}\pi^{\mathrm{2}} }{\mathrm{18}}\:=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{18}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{9}} \\ $$
