Menu Close

0-1-ln-x-1-x-2-x-dx-pi-2-16-

Tinku Tara 0 Comments
Pin




Question Number 136765 by Ñï= last updated on 25/Mar/21
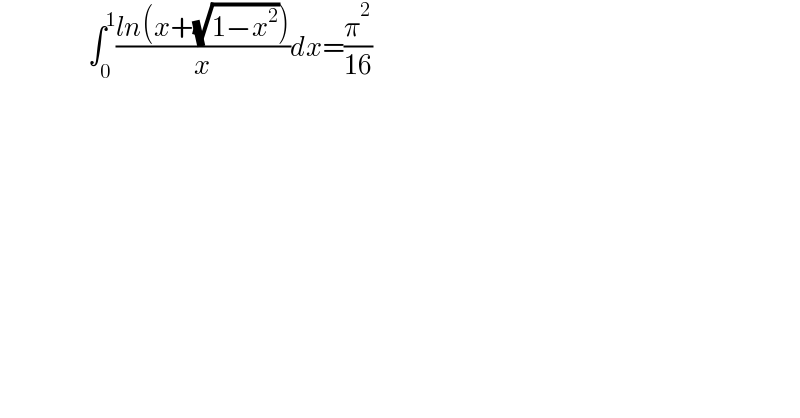
∫_0 ^1 ((ln(x+(√(1−x^2 ))))/x)dx=(π^2 /(16))
$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}{{x}}{dx}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$
Answered by snipers237 last updated on 25/Mar/21
let named it A by stating x=sint A=∫_0 ^(π/2) ((ln(sint+cost))/(tant))dt =∫_0 ^(π/2) tant .ln(sint+cost)dt due to (π/2)−t stability 2A=∫_0 ^(π/2) (tant+(1/(tant)))ln(sint+cost)dt 2A=∫_(0 ) ^(π/2) ((2ln(sint+cost))/(sin2t))dt=∫_0 ^(π/2) ((ln(1+sin2t))/(sin(2t)))dt 4A=∫_0 ^π ((ln(1+sint))/(sint))dt Let g(a)=∫_0 ^(π ) ((ln(1+asint))/(sint))dt g^′ (a)= ∫_0 ^π ((sint dt)/(sint(1+asint))) =∫_0 ^π (a^(−1) /(a^(−1) +sint))dt g′(a)= ∫_(−(π/2)) ^(π/2) ((a^(−1) du)/(a^(−1) +cosu)) =2∫_0 ^(π/2) (a^(−1) /(a^(−1) +cosu))du = 2a^(−1) .((2π)/( (√(a^(−2) −1)))) with u=(π/2)−t g′(a)=((4π)/( (√(1−a^2 )) )) .So g(a)=4πarcsin(a) cause g(0)=0 Then g(1)=4πarcsin(1)=2π^2 and A=(π^2 /2)
$${let}\:{named}\:{it}\:{A} \\ $$$${by}\:{stating}\:{x}={sint}\:\:\: \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{ln}\left({sint}+{cost}\right)}{{tant}}{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{tant}\:.{ln}\left({sint}+{cost}\right){dt}\:\:{due}\:{to}\:\frac{\pi}{\mathrm{2}}−{t}\:{stability} \\ $$$$\mathrm{2}{A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({tant}+\frac{\mathrm{1}}{{tant}}\right){ln}\left({sint}+{cost}\right){dt} \\ $$$$\mathrm{2}{A}=\int_{\mathrm{0}\:\:} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{2}{ln}\left({sint}+{cost}\right)}{{sin}\mathrm{2}{t}}{dt}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}+{sin}\mathrm{2}{t}\right)}{{sin}\left(\mathrm{2}{t}\right)}{dt} \\ $$$$\mathrm{4}{A}=\int_{\mathrm{0}} ^{\pi} \frac{{ln}\left(\mathrm{1}+{sint}\right)}{{sint}}{dt} \\ $$$${Let}\:\:{g}\left({a}\right)=\int_{\mathrm{0}} ^{\pi\:} \frac{{ln}\left(\mathrm{1}+{asint}\right)}{{sint}}{dt} \\ $$$$\:{g}^{'} \left({a}\right)=\:\int_{\mathrm{0}} ^{\pi} \:\frac{{sint}\:{dt}}{{sint}\left(\mathrm{1}+{asint}\right)}\:=\int_{\mathrm{0}} ^{\pi} \frac{{a}^{−\mathrm{1}} }{{a}^{−\mathrm{1}} +{sint}}{dt} \\ $$$${g}'\left({a}\right)=\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{a}^{−\mathrm{1}} {du}}{{a}^{−\mathrm{1}} +{cosu}}\:=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{a}^{−\mathrm{1}} }{{a}^{−\mathrm{1}} +{cosu}}{du}\:=\:\mathrm{2}{a}^{−\mathrm{1}} .\frac{\mathrm{2}\pi}{\:\sqrt{{a}^{−\mathrm{2}} −\mathrm{1}}}\:\:\:\:\:\:\:\:\:\:\:\:\:{with}\:\:\:{u}=\frac{\pi}{\mathrm{2}}−{t} \\ $$$${g}'\left({a}\right)=\frac{\mathrm{4}\pi}{\:\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\:}\:.{So}\:\:\:{g}\left({a}\right)=\mathrm{4}\pi{arcsin}\left({a}\right)\:{cause}\:{g}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${Then}\:\:{g}\left(\mathrm{1}\right)=\mathrm{4}\pi{arcsin}\left(\mathrm{1}\right)=\mathrm{2}\pi^{\mathrm{2}} \: \\ $$$${and}\:\:\:{A}=\frac{\pi^{\mathrm{2}} }{\mathrm{2}}\: \\ $$$$ \\ $$
Answered by Ñï= last updated on 26/Mar/21
∫_0 ^1 ((ln(x+(√(1−x^2 ))))/x)dx=∫_0 ^(π/2) ((ln(sin x+cos x))/(tan ))dx =∫_0 ^(π/2) ((ln (1+tan x))/(tan x))dx+∫_0 ^(π/2) ((ln cos x)/(tan x))dx =∫_0 ^∞ ((ln (1+x))/(x(1+x^2 )))dx+∫_0 ^1 ((yln y)/(1−y^2 ))dy =∫_0 ^1 ((ln (1+x))/(x(1+x^2 )))dx+∫_1 ^∞ ((ln (1+x))/(x(1+x^2 )))dx+Σ_(n=0) ^∞ ∫_0 ^1 y^(2n+1) ln ydy =∫_0 ^1 ((ln (1+x))/(x(1+x^2 )))dx+∫_0 ^1 ((xln (1+x)−xln x)/(1+x^2 ))dx−Σ_(n=0) ^∞ (1/(4(n+1)^2 )) =∫_0 ^1 ((ln (1+x))/(x(1+x^2 )))dx+∫_0 ^1 [(1/x)(1−(1/((1+x^2 ))))]ln (1+x)−((xln x)/(1+x^2 ))dx−(π^2 /(24)) =∫_0 ^1 ((ln (1+x))/x)dx−Σ_(n=0) ^∞ (−1)^n ∫_0 ^1 x^(2n+1) lnxdx−(π^2 /(24)) =(π^2 /(24))+Σ_(n=0) ^∞ (((−1)^n )/(4(n+1)^2 ))=(π^2 /(24))+(1−2^(1−2) )(π^2 /(24))=(π^2 /(16))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)}{{x}}{dx}=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\left(\mathrm{sin}\:{x}+\mathrm{cos}\:{x}\right)}{\mathrm{tan}\:}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\:\left(\mathrm{1}+\mathrm{tan}\:{x}\right)}{\mathrm{tan}\:{x}}{dx}+\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ln}\:\mathrm{cos}\:{x}}{\mathrm{tan}\:{x}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{ln}\:\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{yln}\:{y}}{\mathrm{1}−{y}^{\mathrm{2}} }{dy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\:\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{1}} ^{\infty} \frac{{ln}\:\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\mathrm{1}} {y}^{\mathrm{2}{n}+\mathrm{1}} {ln}\:{ydy} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\:\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{xln}\:\left(\mathrm{1}+{x}\right)−{xln}\:{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{4}\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\:\left(\mathrm{1}+{x}\right)}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\mathrm{1}}{{x}}\left(\mathrm{1}−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\right)\right]{ln}\:\left(\mathrm{1}+{x}\right)−\frac{{xln}\:{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}−\frac{\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\:\left(\mathrm{1}+{x}\right)}{{x}}{dx}−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}{n}+\mathrm{1}} {lnxdx}−\frac{\pi^{\mathrm{2}} }{\mathrm{24}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{4}\left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\pi^{\mathrm{2}} }{\mathrm{24}}+\left(\mathrm{1}−\mathrm{2}^{\mathrm{1}−\mathrm{2}} \right)\frac{\pi^{\mathrm{2}} }{\mathrm{24}}=\frac{\pi^{\mathrm{2}} }{\mathrm{16}} \\ $$
Commented by mnjuly1970 last updated on 26/Mar/21
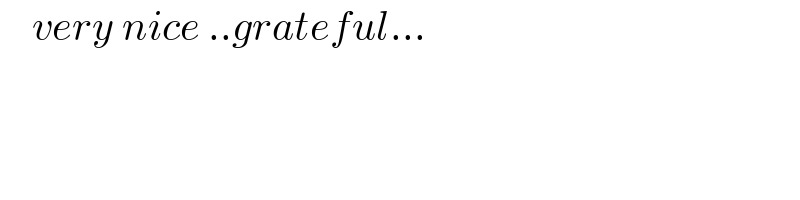
very nice ..grateful...
$$\:\:\:\:{very}\:{nice}\:..{grateful}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *