Question Number 77232 by naka3546 last updated on 04/Jan/20
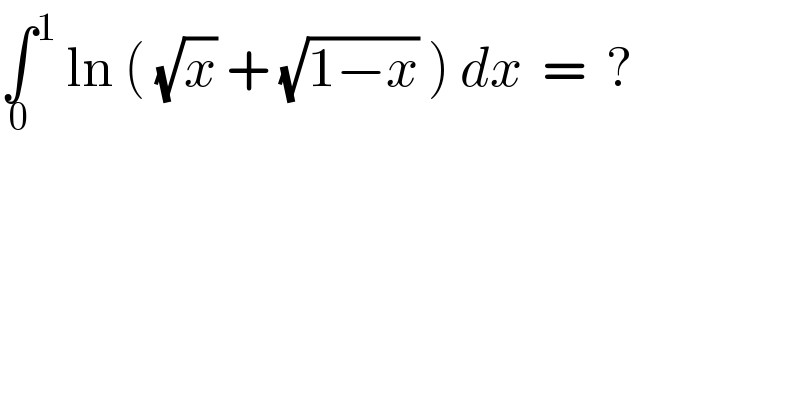
$$\underset{\mathrm{0}} {\int}\overset{\mathrm{1}} {\:}\:\mathrm{ln}\:\left(\:\sqrt{{x}}\:+\:\sqrt{\mathrm{1}−{x}}\:\right)\:{dx}\:\:=\:\:? \\ $$
Answered by MJS last updated on 04/Jan/20
![∫ln ((√x)+(√(1−x))) dx= [t=arcsin (√x) → dx=2(√(x(1−x)))dt] =2∫cos t sin t ln (cos t +sin t) dt= by parts u=ln (cos t +sin t) → u′=((cos t −sin t)/(cos t +sin t)) v′=cos t sin t → v=−(1/2)cos^2 t =−cos^2 t ln (cos t +sin t) +∫((cos t −sin t)/(cos t +sin t))cos^2 t dt= ∫((cos t −sin t)/(cos t +sin t))cos^2 t dt= [u=tan t → dt=cos^2 t du] =−∫((u−1)/((u+1)(u^2 +1)^2 ))du= =−∫(u/((u^2 +1)^2 ))du−(1/2)∫((u−1)/(u^2 +1))du+(1/2)∫(du/(u+1))= =(1/(2(u^2 +1)))−(1/4)ln (u^2 +1) +(1/2)arctan u +(1/2)ln (u+1) = =(1/2)cos^2 t +(1/2)ln cos x +(1/2)t +(1/2)ln (1+tan x) =(1/2)(t+cos^2 t +ln (cos t +sin t)) = =(1/2)(−x+ln ((√x)+(√(1−x)))+arcsin (√x))+C ⇒ answer is (π/4)−(1/2)](https://www.tinkutara.com/question/Q77254.png)
$$\int\mathrm{ln}\:\left(\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{arcsin}\:\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}\left(\mathrm{1}−{x}\right)}{dt}\right] \\ $$$$=\mathrm{2}\int\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}\:\mathrm{ln}\:\left(\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}\right)\:{dt}= \\ $$$$\:\:\:\:\:\mathrm{by}\:\mathrm{parts} \\ $$$$\:\:\:\:\:{u}=\mathrm{ln}\:\left(\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}\right)\:\rightarrow\:{u}'=\frac{\mathrm{cos}\:{t}\:−\mathrm{sin}\:{t}}{\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}} \\ $$$$\:\:\:\:\:{v}'=\mathrm{cos}\:{t}\:\mathrm{sin}\:{t}\:\rightarrow\:{v}=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \:{t} \\ $$$$=−\mathrm{cos}^{\mathrm{2}} \:{t}\:\mathrm{ln}\:\left(\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}\right)\:+\int\frac{\mathrm{cos}\:{t}\:−\mathrm{sin}\:{t}}{\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}}\mathrm{cos}^{\mathrm{2}} \:{t}\:{dt}= \\ $$$$ \\ $$$$\:\:\:\:\:\int\frac{\mathrm{cos}\:{t}\:−\mathrm{sin}\:{t}}{\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}}\mathrm{cos}^{\mathrm{2}} \:{t}\:{dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{u}=\mathrm{tan}\:{t}\:\rightarrow\:{dt}=\mathrm{cos}^{\mathrm{2}} \:{t}\:{du}\right] \\ $$$$\:\:\:\:\:=−\int\frac{{u}−\mathrm{1}}{\left({u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du}= \\ $$$$\:\:\:\:\:=−\int\frac{{u}}{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{du}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{u}−\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}{du}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}+\mathrm{1}}= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}\left({u}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({u}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:{u}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({u}+\mathrm{1}\right)\:= \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}^{\mathrm{2}} \:{t}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{cos}\:{x}\:+\frac{\mathrm{1}}{\mathrm{2}}{t}\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{1}+\mathrm{tan}\:{x}\right) \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({t}+\mathrm{cos}^{\mathrm{2}} \:{t}\:+\mathrm{ln}\:\left(\mathrm{cos}\:{t}\:+\mathrm{sin}\:{t}\right)\right)\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(−{x}+\mathrm{ln}\:\left(\sqrt{{x}}+\sqrt{\mathrm{1}−{x}}\right)+\mathrm{arcsin}\:\sqrt{{x}}\right)+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\pi}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by naka3546 last updated on 04/Jan/20
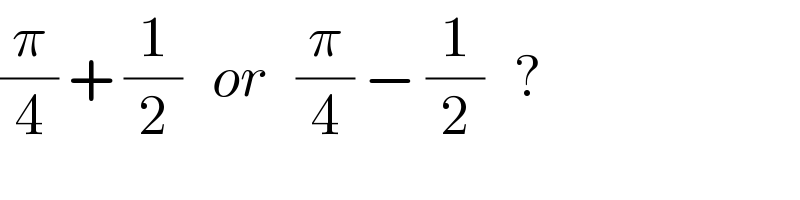
$$\frac{\pi}{\mathrm{4}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:{or}\:\:\:\frac{\pi}{\mathrm{4}}\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\:\:? \\ $$
Commented by MJS last updated on 04/Jan/20

$$− \\ $$$$\mathrm{sorry}\:\mathrm{typo} \\ $$
