Menu Close

0-1-log-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 135127 by Dwaipayan Shikari last updated on 10/Mar/21
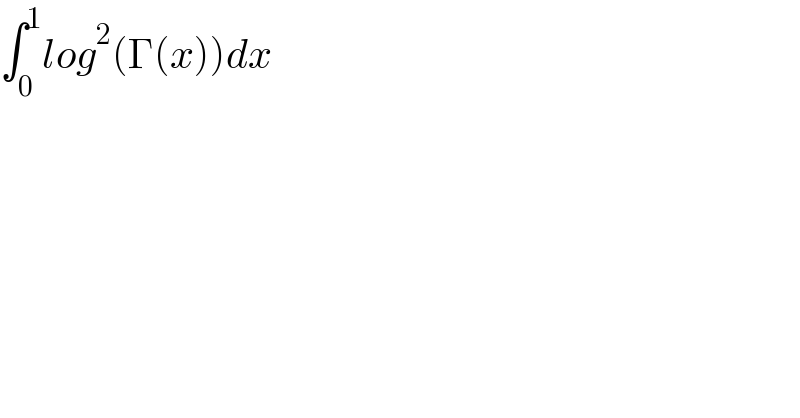
∫_0 ^1 log^2 (Γ(x))dx
$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}^{\mathrm{2}} \left(\Gamma\left({x}\right)\right){dx} \\ $$
Answered by mathmax by abdo last updated on 11/Mar/21
we have Γ(x).Γ(1−x)=(π/(sin(πx))) ⇒ log(Γ(x))+log(Γ(1−x))=log(π)−log(sin(πx)) ⇒ log(Γ(x))^2 +2log(Γ(x))log(Γ(1−x))+log^2 (Γ(1−x)) =log^2 (π)−2logπ log(sin(πx))+log^2 (sin(πx)) ⇒ ∫_0 ^1 log^2 (Γ(x))dx+∫_0 ^1 log^2 (Γ(1−x))dx+2∫_0 ^1 log(Γ(x))log(Γ(1−x))dx =log^2 (π)−2logπ ∫_0 ^1 log(sin(πx))dx+∫_0 ^1 log^2 (sin(πx))dx ∫_0 ^1 log^2 (Γ(1−x))dx =_(1−x=t) ∫_0 ^1 log^2 (Γ(t))dt ∫_0 ^1 log(sin(πx))dx =_(πx=t) (1/π) ∫_0 ^π log(sint)dt =(1/π)∫_0 ^(π/2) log(sint)dt +(1/π)∫_(π/2) ^π log(sint)dt (→t=(π/2)+u) =(1/π)(−(π/2)log2)+(1/π)(−(π/2)log2) =−log(2) ⇒2∫_0 ^1 log^2 (Γ(x))dx+2∫_0 ^1 log(Γ(x)).log(Γ(1−x))dx =log^2 π+2logπlog2 +∫_0 ^1 log^2 (sin(πx))dx ...be continued...
$$\mathrm{we}\:\mathrm{have}\:\Gamma\left(\mathrm{x}\right).\Gamma\left(\mathrm{1}−\mathrm{x}\right)=\frac{\pi}{\mathrm{sin}\left(\pi\mathrm{x}\right)}\:\Rightarrow \\ $$$$\mathrm{log}\left(\Gamma\left(\mathrm{x}\right)\right)+\mathrm{log}\left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)=\mathrm{log}\left(\pi\right)−\mathrm{log}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\:\Rightarrow \\ $$$$\mathrm{log}\left(\Gamma\left(\mathrm{x}\right)\right)^{\mathrm{2}} \:+\mathrm{2log}\left(\Gamma\left(\mathrm{x}\right)\right)\mathrm{log}\left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)+\mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right) \\ $$$$=\mathrm{log}^{\mathrm{2}} \left(\pi\right)−\mathrm{2log}\pi\:\mathrm{log}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)+\mathrm{log}^{\mathrm{2}} \left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{x}\right)\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{dx}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\Gamma\left(\mathrm{x}\right)\right)\mathrm{log}\left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\mathrm{log}^{\mathrm{2}} \left(\pi\right)−\mathrm{2log}\pi\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{dx}\:=_{\mathrm{1}−\mathrm{x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{t}\right)\right)\mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{log}\left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\mathrm{dx}\:=_{\pi\mathrm{x}=\mathrm{t}} \:\frac{\mathrm{1}}{\pi}\:\int_{\mathrm{0}} ^{\pi} \mathrm{log}\left(\mathrm{sint}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\pi}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{log}\left(\mathrm{sint}\right)\mathrm{dt}\:+\frac{\mathrm{1}}{\pi}\int_{\frac{\pi}{\mathrm{2}}} ^{\pi} \mathrm{log}\left(\mathrm{sint}\right)\mathrm{dt}\:\left(\rightarrow\mathrm{t}=\frac{\pi}{\mathrm{2}}+\mathrm{u}\right) \\ $$$$=\frac{\mathrm{1}}{\pi}\left(−\frac{\pi}{\mathrm{2}}\mathrm{log2}\right)+\frac{\mathrm{1}}{\pi}\left(−\frac{\pi}{\mathrm{2}}\mathrm{log2}\right)\:=−\mathrm{log}\left(\mathrm{2}\right) \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \left(\Gamma\left(\mathrm{x}\right)\right)\mathrm{dx}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{log}\left(\Gamma\left(\mathrm{x}\right)\right).\mathrm{log}\left(\Gamma\left(\mathrm{1}−\mathrm{x}\right)\right)\mathrm{dx} \\ $$$$=\mathrm{log}^{\mathrm{2}} \pi+\mathrm{2log}\pi\mathrm{log2}\:+\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \left(\mathrm{sin}\left(\pi\mathrm{x}\right)\right)\mathrm{dx}\:\:…\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *