Question Number 65681 by aliesam last updated on 01/Aug/19
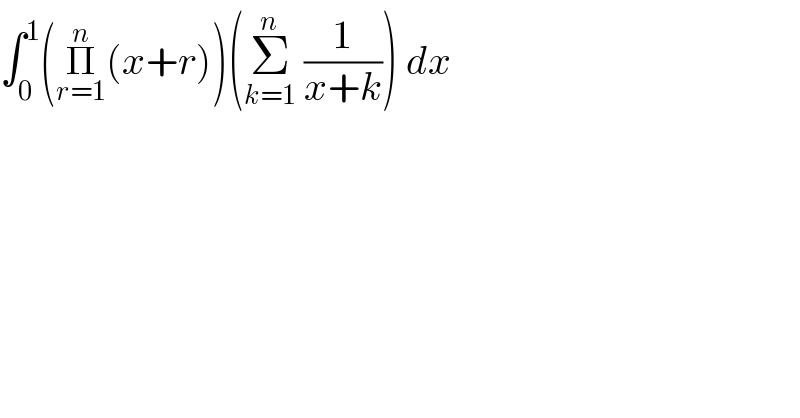
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}\left({x}+{r}\right)\right)\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{x}+{k}}\right)\:{dx} \\ $$
Answered by Tanmay chaudhury last updated on 02/Aug/19
![∫_0 ^1 (x+1)(x+2)(x+3)...(x+n)×((1/(x+1))+(1/(x+2))+(1/(x+3))+...+(1/(x+n)))dx y=(x+1)(x+2)(x+3)...(x+n) lny=ln(x+1)+ln(x+2)+ln(x+3)+..+ln(x+n) (1/y)×(dy/dx)=(1/(x+1))+(1/(x+2))+(1/(x+3))+..+(1/(x+n)) (dy/dx)=(x+1)(x+2)(x+3)...(x+n)×((1/(x+1))+(1/(x+2))+..+(1/(x+n))) dy=[Π_(r=1) ^n (x+r)×Σ_(n=1) ^n (1/(x+r))]dx ∫_0 ^1 Π(x+r)×Σ_(k=1) ^n (1/(x+k))dx =∫_0 ^1 d(x+1)(x+2)..(x+n) ∣(x+1)(x+2)(x+3)..(x+n)∣_0 ^1 =(2)(3)(4)...(1+n)−(1×2×3..×n) =(n+1)!−n! =(n+1)!−n! =(n+1)n!−n! =(n+1−1)×n! =n×n!](https://www.tinkutara.com/question/Q65725.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)…\left({x}+{n}\right)×\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{2}}+\frac{\mathrm{1}}{{x}+\mathrm{3}}+…+\frac{\mathrm{1}}{{x}+{n}}\right){dx} \\ $$$${y}=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)…\left({x}+{n}\right) \\ $$$${lny}={ln}\left({x}+\mathrm{1}\right)+{ln}\left({x}+\mathrm{2}\right)+{ln}\left({x}+\mathrm{3}\right)+..+{ln}\left({x}+{n}\right) \\ $$$$\frac{\mathrm{1}}{{y}}×\frac{{dy}}{{dx}}=\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{2}}+\frac{\mathrm{1}}{{x}+\mathrm{3}}+..+\frac{\mathrm{1}}{{x}+{n}} \\ $$$$\frac{{dy}}{{dx}}=\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)…\left({x}+{n}\right)×\left(\frac{\mathrm{1}}{{x}+\mathrm{1}}+\frac{\mathrm{1}}{{x}+\mathrm{2}}+..+\frac{\mathrm{1}}{{x}+{n}}\right) \\ $$$${dy}=\left[\underset{{r}=\mathrm{1}} {\overset{{n}} {\prod}}\left({x}+{r}\right)×\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{x}+{r}}\right]{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \Pi\left({x}+{r}\right)×\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{x}+{k}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {d}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)..\left({x}+{n}\right) \\ $$$$\mid\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)..\left({x}+{n}\right)\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\left(\mathrm{2}\right)\left(\mathrm{3}\right)\left(\mathrm{4}\right)…\left(\mathrm{1}+{n}\right)−\left(\mathrm{1}×\mathrm{2}×\mathrm{3}..×{n}\right) \\ $$$$=\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$=\left({n}+\mathrm{1}\right)!−{n}! \\ $$$$=\left({n}+\mathrm{1}\right){n}!−{n}! \\ $$$$=\left({n}+\mathrm{1}−\mathrm{1}\right)×{n}! \\ $$$$={n}×{n}! \\ $$$$ \\ $$
