Question Number 142488 by rs4089 last updated on 01/Jun/21

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{k}−\mathrm{1}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$
Answered by Ar Brandon last updated on 01/Jun/21
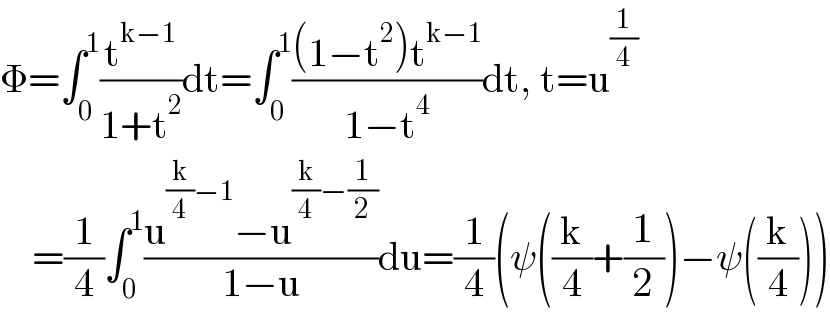
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{t}^{\mathrm{k}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{t}^{\mathrm{k}−\mathrm{1}} }{\mathrm{1}−\mathrm{t}^{\mathrm{4}} }\mathrm{dt},\:\mathrm{t}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{\frac{\mathrm{k}}{\mathrm{4}}−\mathrm{1}} −\mathrm{u}^{\frac{\mathrm{k}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−\mathrm{u}}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{4}}\left(\psi\left(\frac{\mathrm{k}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{k}}{\mathrm{4}}\right)\right) \\ $$
Answered by Dwaipayan Shikari last updated on 01/Jun/21
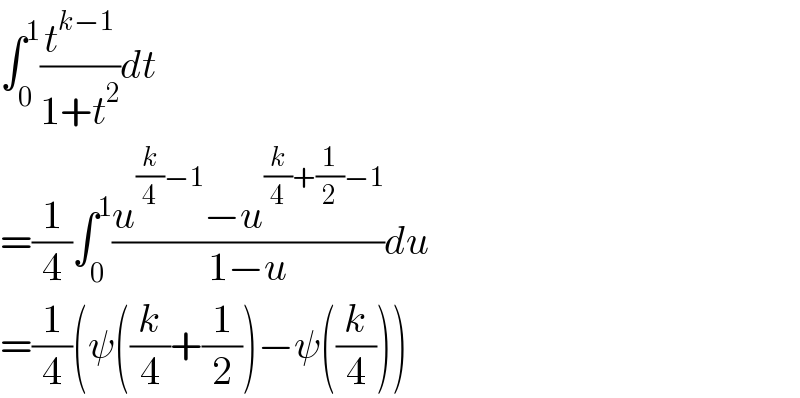
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{{k}−\mathrm{1}} }{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\frac{{k}}{\mathrm{4}}−\mathrm{1}} −{u}^{\frac{{k}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\mathrm{1}−{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\psi\left(\frac{{k}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{{k}}{\mathrm{4}}\right)\right) \\ $$
