Question Number 70718 by oyemi kemewari last updated on 07/Oct/19
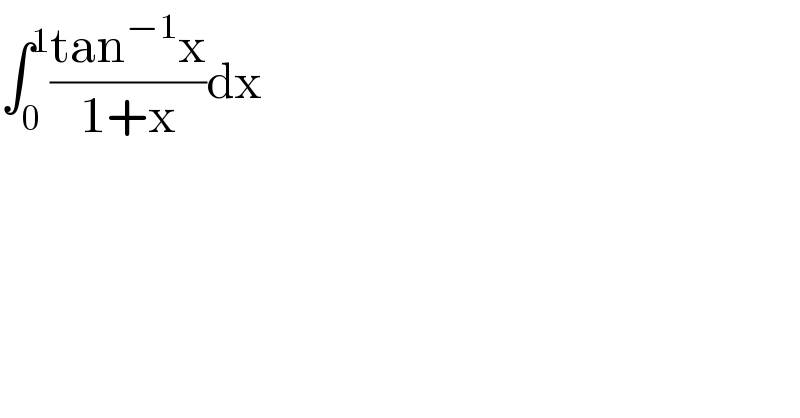
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{x}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$
Commented by mathmax by abdo last updated on 07/Oct/19
![let I =∫_0 ^1 ((arctan(x))/(1+x))dx and f(t)=∫_0 ^1 ((arctan(tx))/(1+x))dx with t≥0 I=f(1) and f^′ (t)= ∫_0 ^1 (x/((1+x^2 t^2 )(1+x)))dx =_(xt=u) ∫_0 ^t (u/(t(1+u^2 )(1+(u/t)))) (du/t) =∫_0 ^t (u/(t(1+u^2 )(t+u)))du =(1/t) ∫_0 ^t ((udu)/((u+t)(u^2 +1))) let decompose F(u)=(u/((u+t)(u^2 +1))) F(u)=(a/(u+t)) +((bu +c)/(u^2 +1)) a=lim_(u→−t) (u+t)F(u)=((−t)/(t^2 +1)) lim_(u→+∞) uF(u)=0 =a+b ⇒b=(t/(t^2 +1)) ⇒ F(u)=((−t)/((t^2 +1)(u+t))) +((((tu)/(t^2 +1))+c)/(u^2 +1)) F(0)=0=((−t)/(t(t^2 +1))) +c =−(1/(t^2 +1)) +c ⇒c=(1/(t^2 +1)) ⇒ F(u)=(1/(t^2 +1)){((−t)/(u+t)) +((tu +1)/(u^2 +1))} ⇒ f^′ (t)=∫_0 ^t F(u)du =((−t)/(t^2 +1)) ∫_0 ^t (du/(u+t)) +(1/(t^2 +1))(t/2) ∫_0 ^t ((2u)/(u^2 +1))du+(1/(t^2 +1))∫_0 ^t (du/(u^2 +1)) =−(t/(t^2 +1))[ln(u+t)]_0 ^t +(t/(2(t^2 +1)))[ln(u^2 +1)]_0 ^t +((arctan(t))/(t^2 +1)) =((−tln(2))/(t^2 +1)) +((tln(t^2 +1))/(2(t^2 +1))) +((arctan(t))/(t^2 +1)) ⇒ f(t)=−ln(2)∫_0 ^t (x/(x^2 +1))dx +∫_0 ^t ((xln(x^2 +1))/(2(x^2 +1)))dx +∫_0 ^t ((arctan(x))/(x^2 +1))dx +c .....be continued...](https://www.tinkutara.com/question/Q70731.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}}{dx}\:\:{and}\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{arctan}\left({tx}\right)}{\mathrm{1}+{x}}{dx}\:\:{with}\:{t}\geqslant\mathrm{0} \\ $$$${I}={f}\left(\mathrm{1}\right)\:\:{and}\:{f}^{'} \left({t}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}}{\left(\mathrm{1}+{x}^{\mathrm{2}} {t}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}\right)}{dx} \\ $$$$=_{{xt}={u}} \:\:\:\:\:\:\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{u}}{{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{{u}}{{t}}\right)}\:\frac{{du}}{{t}}\:=\int_{\mathrm{0}} ^{{t}} \:\:\:\frac{{u}}{{t}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\left({t}+{u}\right)}{du} \\ $$$$=\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{{udu}}{\left({u}+{t}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)}\:\:{let}\:{decompose}\:{F}\left({u}\right)=\frac{{u}}{\left({u}+{t}\right)\left({u}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$${F}\left({u}\right)=\frac{{a}}{{u}+{t}}\:+\frac{{bu}\:+{c}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}={lim}_{{u}\rightarrow−{t}} \:\:\:\left({u}+{t}\right){F}\left({u}\right)=\frac{−{t}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${lim}_{{u}\rightarrow+\infty} {uF}\left({u}\right)=\mathrm{0}\:={a}+{b}\:\Rightarrow{b}=\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{−{t}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left({u}+{t}\right)}\:+\frac{\frac{{tu}}{{t}^{\mathrm{2}} +\mathrm{1}}+{c}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}=\frac{−{t}}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\:+{c}\:=−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+{c}\:\Rightarrow{c}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left\{\frac{−{t}}{{u}+{t}}\:+\frac{{tu}\:+\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\right\}\:\Rightarrow \\ $$$${f}^{'} \left({t}\right)=\int_{\mathrm{0}} ^{{t}} {F}\left({u}\right){du}\:=\frac{−{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\int_{\mathrm{0}} ^{{t}} \:\:\frac{{du}}{{u}+{t}}\:+\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\frac{{t}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{t}} \frac{\mathrm{2}{u}}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du}+\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\int_{\mathrm{0}} ^{{t}} \:\frac{{du}}{{u}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=−\frac{{t}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\left[{ln}\left({u}+{t}\right)\right]_{\mathrm{0}} ^{{t}} \:\:+\frac{{t}}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\left[{ln}\left({u}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{{t}} \:+\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$=\frac{−{tln}\left(\mathrm{2}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{tln}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\mathrm{2}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)}\:+\frac{{arctan}\left({t}\right)}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$${f}\left({t}\right)=−{ln}\left(\mathrm{2}\right)\int_{\mathrm{0}} ^{{t}} \:\:\frac{{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx}\:+\int_{\mathrm{0}} ^{{t}} \:\:\frac{{xln}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}{\mathrm{2}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}{dx}\:\:+\int_{\mathrm{0}} ^{{t}} \:\frac{{arctan}\left({x}\right)}{{x}^{\mathrm{2}} \:+\mathrm{1}}{dx} \\ $$$$+{c}\:…..{be}\:{continued}… \\ $$
Answered by mind is power last updated on 07/Oct/19
![x=tg(u) ⇒dx=(du/(cos^2 (u))) I=∫_0 ^1 ((tan^(−1) (x))/(1+x))dd=∫_0 ^(π/4) (u/((1+tg(u)))).(1/(cos^2 (u)))=∫_0 ^(π/4) ((udu)/((sin(u)+cos(u))(cos(u)))) cos(u)+sin(u)=(√2)(cos(u−(π/4))) I=∫_0 ^(π/4) ((udu)/( (√2)cos(u−(π/4))cos(u))) let f(u)=(u/( (√2)cos(u−(π/4))cos(u))) i will use this in the next step∫_a ^b f(x)dx=∫_a ^b f(a+b−x)dx ⇒I=∫_0 ^(π/4) (((π/4)−u)/( (√2)cos((π/4)−u−(π/4)).cos((π/4)−u)))du I=∫_0 ^u ((−udu)/( (√2)cos(u)cos((π/4)−u)))+(π/4)∫_0 ^(π/4) (du/( (√2)cos((π/4)−u)cos(u))) ⇒I=−(1/( (√2))).I+(π/4)∫_0 ^(π/4) (du/((cos(u)+sin(u))cos(u))) ⇒I=((√2)/( (√(2+))1)).(π/4)∫_0 ^(π/4) ((1.du)/((cos(u)+sin(u))cos(u))) 1=(cos(u)+sin(u))^2 −2sin(u)cos(u) A=∫_0 ^(π/4) ((1.du)/((cos(u)+sin(u))cos(u)))=∫_0 ^(π/4) (((cos(u)+sin(u))^2 −2cos(u)sin(u))/((sin(u)+cos(u))cos(u))) =∫_0 ^(π/4) ((cos(u)+sin(u))/(cos(u)))du−∫_0 ^(π/4) ((2sin(u))/(cos(u)+sin(u)))du sin(u)=−(cos(u)−sin(u)+(sin(u)+cos(u)) =∫_0 ^(π/4) (1+tg(u))du−∫_0 ^(π/4) ((−(cos(u)−sin(u))+(sin(u)+cos(u))du)/(cos(u)+sin(u))) ∫_0 ^(π/4) (1+tg(u))du+∫_0 ^(π/4) ((cos(u)−sin(u))/(cos(u)+sin(u)))du−∫1du =∫_0 ^(π/4) tg(u)du+∫_0 ^(π/4) ((d(sin(u)+cos(u)))/(cos(u)+sin(u))) =_0 ^(π/4) [−ln(cos(u))+ln(cos(u)+sin(u))] =−ln(((√2)/2))+ln((√2))=ln(2) I=((√2)/( (√2)+1)).(π/4).A=((π.ln(2)(√2))/(4((√2)+1)))](https://www.tinkutara.com/question/Q70730.png)
$$\mathrm{x}=\mathrm{tg}\left(\mathrm{u}\right) \\ $$$$\Rightarrow{dx}=\frac{\mathrm{du}}{\mathrm{cos}\:^{\mathrm{2}} \left(\mathrm{u}\right)} \\ $$$$\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{x}\right)}{\mathrm{1}+\mathrm{x}}\mathrm{dd}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{u}}{\left(\mathrm{1}+{tg}\left({u}\right)\right)}.\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \left({u}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{udu}}{\left({sin}\left({u}\right)+{cos}\left({u}\right)\right)\left({cos}\left({u}\right)\right)} \\ $$$${cos}\left({u}\right)+{sin}\left({u}\right)=\sqrt{\mathrm{2}}\left({cos}\left({u}−\frac{\pi}{\mathrm{4}}\right)\right) \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{udu}}{\:\sqrt{\mathrm{2}}{cos}\left({u}−\frac{\pi}{\mathrm{4}}\right){cos}\left({u}\right)} \\ $$$${let}\:{f}\left({u}\right)=\frac{{u}}{\:\sqrt{\mathrm{2}}{cos}\left({u}−\frac{\pi}{\mathrm{4}}\right){cos}\left({u}\right)} \\ $$$${i}\:{will}\:{use}\:{this}\:{in}\:{the}\:{next}\:{step}\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\int_{{a}} ^{{b}} {f}\left({a}+{b}−{x}\right){dx} \\ $$$$\Rightarrow{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\frac{\pi}{\mathrm{4}}−{u}}{\:\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}−{u}−\frac{\pi}{\mathrm{4}}\right).{cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}{du} \\ $$$${I}=\int_{\mathrm{0}} ^{{u}} \frac{−{udu}}{\:\sqrt{\mathrm{2}}{cos}\left({u}\right){cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right)}+\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{du}}{\:\sqrt{\mathrm{2}}{cos}\left(\frac{\pi}{\mathrm{4}}−{u}\right){cos}\left({u}\right)} \\ $$$$\Rightarrow{I}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}.{I}+\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{du}}{\left({cos}\left({u}\right)+{sin}\left({u}\right)\right){cos}\left({u}\right)} \\ $$$$\Rightarrow{I}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}+}\mathrm{1}}.\frac{\pi}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}.{du}}{\left({cos}\left({u}\right)+{sin}\left({u}\right)\right){cos}\left({u}\right)} \\ $$$$\mathrm{1}=\left({cos}\left({u}\right)+{sin}\left({u}\right)\right)^{\mathrm{2}} −\mathrm{2}{sin}\left({u}\right){cos}\left({u}\right) \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}.{du}}{\left({cos}\left({u}\right)+{sin}\left({u}\right)\right){cos}\left({u}\right)}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\left({cos}\left({u}\right)+{sin}\left({u}\right)\right)^{\mathrm{2}} −\mathrm{2}{cos}\left({u}\right){sin}\left({u}\right)}{\left({sin}\left({u}\right)+{cos}\left({u}\right)\right){cos}\left({u}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{cos}\left({u}\right)+{sin}\left({u}\right)}{{cos}\left({u}\right)}{du}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{2}{sin}\left({u}\right)}{{cos}\left({u}\right)+{sin}\left({u}\right)}{du} \\ $$$${sin}\left({u}\right)=−\left({cos}\left({u}\right)−{sin}\left({u}\right)+\left({sin}\left({u}\right)+{cos}\left({u}\right)\right)\right. \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+{tg}\left({u}\right)\right){du}−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{−\left({cos}\left({u}\right)−{sin}\left({u}\right)\right)+\left({sin}\left({u}\right)+{cos}\left({u}\right)\right){du}}{{cos}\left({u}\right)+{sin}\left({u}\right)} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+{tg}\left({u}\right)\right){du}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{cos}\left({u}\right)−{sin}\left({u}\right)}{{cos}\left({u}\right)+{sin}\left({u}\right)}{du}−\int\mathrm{1}{du} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tg}\left({u}\right){du}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{d}\left({sin}\left({u}\right)+{cos}\left({u}\right)\right)}{{cos}\left({u}\right)+{sin}\left({u}\right)} \\ $$$$=_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left[−{ln}\left({cos}\left({u}\right)\right)+{ln}\left({cos}\left({u}\right)+{sin}\left({u}\right)\right)\right] \\ $$$$=−{ln}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)+{ln}\left(\sqrt{\mathrm{2}}\right)={ln}\left(\mathrm{2}\right) \\ $$$${I}=\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}.\frac{\pi}{\mathrm{4}}.{A}=\frac{\pi.{ln}\left(\mathrm{2}\right)\sqrt{\mathrm{2}}}{\mathrm{4}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$ \\ $$$$ \\ $$
Commented by oyemi kemewari last updated on 07/Oct/19
thank you sir
Commented by mind is power last updated on 07/Oct/19

$${y}'{re}\:{welcom} \\ $$
Commented by oyemi kemewari last updated on 08/Oct/19
thank you sir
