Question Number 7585 by Tawakalitu. last updated on 04/Sep/16
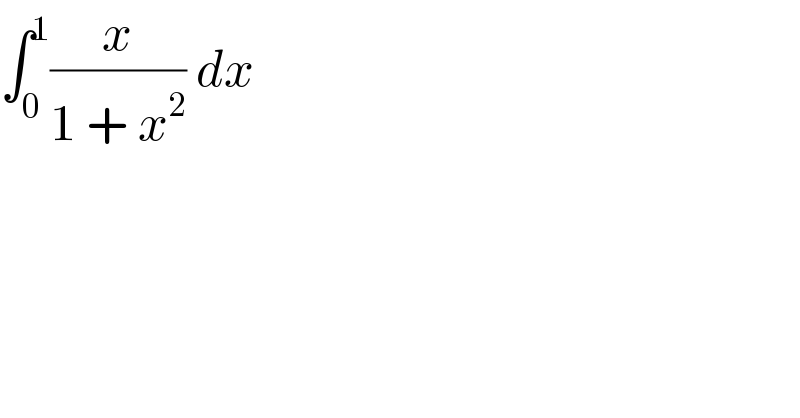
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}\:+\:{x}^{\mathrm{2}} }\:{dx} \\ $$
Commented by sou1618 last updated on 05/Sep/16
![∫_0 ^1 (1/2)×((2x)/(x^2 +1))dx=(1/2)∫_0 ^1 ln(x^2 +1)′dx =(1/2)[ln(x^2 +1)]_0 ^1 =((ln2)/2)](https://www.tinkutara.com/question/Q7586.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)'{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{{ln}\mathrm{2}}{\mathrm{2}} \\ $$
Commented by Tawakalitu. last updated on 05/Sep/16

$${Thank}\:{you}\:{sir} \\ $$
Commented by FilupSmith last updated on 05/Sep/16
![another way to write it. exactly the same as above u=x^2 +1 du=2xdx xdx=(1/2)du ∫_0 ^( 1) ((xdx)/(x^2 +1))=∫_(x=0) ^( x=1) (1/2) (1/u)du =(1/2)[ln(u)]_(x=0) ^(x=1) =(1/2)[ln(x^2 +1)]_0 ^1 =(1/2)(ln(2)+ln(1)) =(1/2)ln(2)](https://www.tinkutara.com/question/Q7596.png)
$$\mathrm{another}\:\mathrm{way}\:\mathrm{to}\:\mathrm{write}\:\mathrm{it}. \\ $$$$\mathrm{exactly}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{above} \\ $$$${u}={x}^{\mathrm{2}} +\mathrm{1}\: \\ $$$${du}=\mathrm{2}{xdx} \\ $$$${xdx}=\frac{\mathrm{1}}{\mathrm{2}}{du} \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{xdx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}}{{u}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left({u}\right)\right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{ln}\left(\mathrm{1}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right) \\ $$
Commented by Tawakalitu. last updated on 05/Sep/16

$${Thank}\:{you}\:{sir}. \\ $$
Commented by 123456 last updated on 05/Sep/16
![also u=x^2 +1 x=0⇒u=1 x=1⇒u=2 ∫_(x=0) ^(x=1) ((xdx)/(x^2 +1))=∫_(u=1) ^(u=2) (du/(2u))=(([ln u]_(u=1) ^(u=2) )/2)=((ln 2)/2)](https://www.tinkutara.com/question/Q7607.png)
$$\mathrm{also} \\ $$$${u}={x}^{\mathrm{2}} +\mathrm{1} \\ $$$${x}=\mathrm{0}\Rightarrow{u}=\mathrm{1} \\ $$$${x}=\mathrm{1}\Rightarrow{u}=\mathrm{2} \\ $$$$\underset{{x}=\mathrm{0}} {\overset{{x}=\mathrm{1}} {\int}}\frac{{xdx}}{{x}^{\mathrm{2}} +\mathrm{1}}=\underset{{u}=\mathrm{1}} {\overset{{u}=\mathrm{2}} {\int}}\frac{{du}}{\mathrm{2}{u}}=\frac{\left[\mathrm{ln}\:{u}\right]_{{u}=\mathrm{1}} ^{{u}=\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$
