Question Number 137123 by bobhans last updated on 30/Mar/21
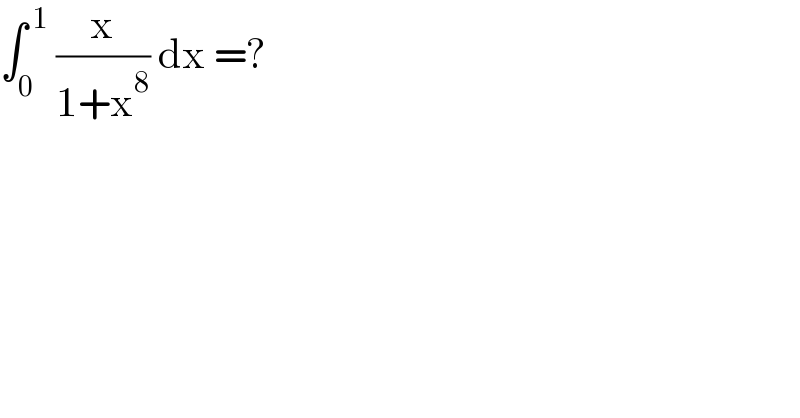
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{8}} }\:\mathrm{dx}\:=? \\ $$
Commented by Ar Brandon last updated on 30/Mar/21
You're right, Sir. Greetings to you !
It's been quite a longtime since we last interracted. Haha !
Commented by MJS_new last updated on 30/Mar/21
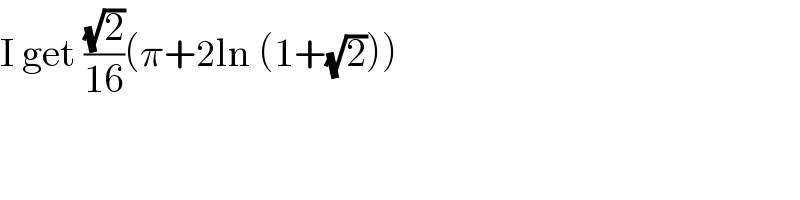
$$\mathrm{I}\:\mathrm{get}\:\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\left(\pi+\mathrm{2ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right) \\ $$
Commented by bobhans last updated on 30/Mar/21
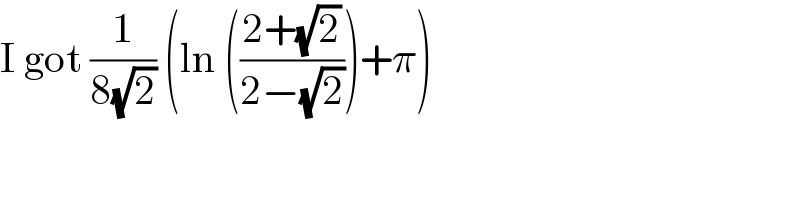
$$\mathrm{I}\:\mathrm{got}\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}\:\left(\mathrm{ln}\:\left(\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\right)+\pi\right) \\ $$
Commented by MJS_new last updated on 30/Mar/21
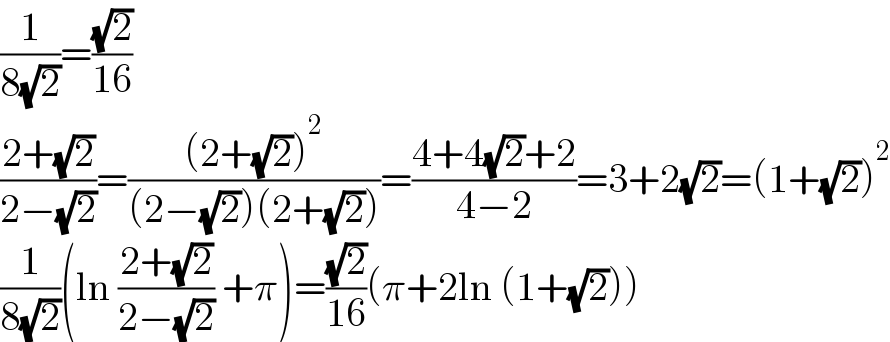
$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{16}} \\ $$$$\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}=\frac{\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}=\frac{\mathrm{4}+\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{2}}{\mathrm{4}−\mathrm{2}}=\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{2}}}\left(\mathrm{ln}\:\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\:+\pi\right)=\frac{\sqrt{\mathrm{2}}}{\mathrm{16}}\left(\pi+\mathrm{2ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\right) \\ $$
Answered by Ar Brandon last updated on 30/Mar/21
![I=∫_0 ^1 (x/(1+x^8 ))dx=^(u=x^8 ) (1/8)∫_0 ^1 (u^(−(6/8)) /(1+u))du=(1/8)∫_0 ^1 ((u^(−(3/4)) (1−u))/(1−u^2 ))du =^(v=u^2 ) (1/(16))∫_0 ^1 ((v^(−(7/8)) (1−v^(1/2) ))/(1−v))dv=(1/(16))[ψ((5/8))−ψ((1/8))]](https://www.tinkutara.com/question/Q137124.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{8}} }\mathrm{dx}\overset{\mathrm{u}=\mathrm{x}^{\mathrm{8}} } {=}\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{−\frac{\mathrm{6}}{\mathrm{8}}} }{\mathrm{1}+\mathrm{u}}\mathrm{du}=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{u}^{−\frac{\mathrm{3}}{\mathrm{4}}} \left(\mathrm{1}−\mathrm{u}\right)}{\mathrm{1}−\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$\:\:\:\overset{\mathrm{v}=\mathrm{u}^{\mathrm{2}} } {=}\frac{\mathrm{1}}{\mathrm{16}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{v}^{−\frac{\mathrm{7}}{\mathrm{8}}} \left(\mathrm{1}−\mathrm{v}^{\frac{\mathrm{1}}{\mathrm{2}}} \right)}{\mathrm{1}−\mathrm{v}}\mathrm{dv}=\frac{\mathrm{1}}{\mathrm{16}}\left[\psi\left(\frac{\mathrm{5}}{\mathrm{8}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{8}}\right)\right] \\ $$
Answered by Ar Brandon last updated on 30/Mar/21
![I=∫_0 ^1 (x/(1+x^8 ))dx=(1/2)∫_0 ^1 ((2x)/(1+x^8 ))dx I=(1/2)∫_0 ^1 (dt/(t^4 +1))=(1/4)∫_0 ^1 (((t^2 +1)−(t^2 −1))/(t^4 +1))dt =(1/4)∫_0 ^1 {((t^2 +1)/(t^4 +1))−((t^2 −1)/(t^4 +1))}dt=(1/4)∫_0 ^1 {((1+(1/t^2 ))/(t^2 +(1/t^2 )))−((1−(1/t^2 ))/(t^2 +(1/t^2 )))}dt =(1/4){∫_0 ^1 ((1+(1/t^2 ))/((t−(1/t))^2 +2))dt−∫_0 ^1 ((1−(1/t^2 ))/((t+(1/t))^2 −2))dt} =(1/4){∫_(−∞) ^0 (du/(u^2 +2))−∫_(+∞) ^2 (dv/(v^2 −2))} =(1/4){[(1/( (√2)))arctan((u/( (√2))))]_(−∞) ^0 +[(1/(2(√2)))ln∣(((√2)+v)/( (√2)−v))∣]_(+∞) ^2 } =(1/4){(0+(π/(2(√2))))+(1/( 2(√2)))(ln∣(((√2)+2)/( (√2)−2))∣)}=(π/(8(√2)))+(1/( 8(√2)))ln∣((1+(√2))/( 1−(√2)))∣](https://www.tinkutara.com/question/Q137132.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}}{\mathrm{1}+\mathrm{x}^{\mathrm{8}} }\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{2x}}{\mathrm{1}+\mathrm{x}^{\mathrm{8}} }\mathrm{dx} \\ $$$$\mathcal{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)−\left(\mathrm{t}^{\mathrm{2}} −\mathrm{1}\right)}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\mathrm{dt} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}−\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{t}^{\mathrm{4}} +\mathrm{1}}\right\}\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{1}} \left\{\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}−\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}\right\}\mathrm{dt} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} +\mathrm{2}}\mathrm{dt}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }}{\left(\mathrm{t}+\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} −\mathrm{2}}\mathrm{dt}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\int_{−\infty} ^{\mathrm{0}} \frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} +\mathrm{2}}−\int_{+\infty} ^{\mathrm{2}} \frac{\mathrm{dv}}{\mathrm{v}^{\mathrm{2}} −\mathrm{2}}\right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left[\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\mathrm{arctan}\left(\frac{\mathrm{u}}{\:\sqrt{\mathrm{2}}}\right)\right]_{−\infty} ^{\mathrm{0}} +\left[\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{v}}{\:\sqrt{\mathrm{2}}−\mathrm{v}}\mid\right]_{+\infty} ^{\mathrm{2}} \right\} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\left\{\left(\mathrm{0}+\frac{\pi}{\mathrm{2}\sqrt{\mathrm{2}}}\right)+\frac{\mathrm{1}}{\:\mathrm{2}\sqrt{\mathrm{2}}}\left(\mathrm{ln}\mid\frac{\sqrt{\mathrm{2}}+\mathrm{2}}{\:\sqrt{\mathrm{2}}−\mathrm{2}}\mid\right)\right\}=\frac{\pi}{\mathrm{8}\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\mathrm{8}\sqrt{\mathrm{2}}}\mathrm{ln}\mid\frac{\mathrm{1}+\sqrt{\mathrm{2}}}{\:\mathrm{1}−\sqrt{\mathrm{2}}}\mid \\ $$
