Menu Close

0-1-x-1-x-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 139296 by mohammad17 last updated on 25/Apr/21
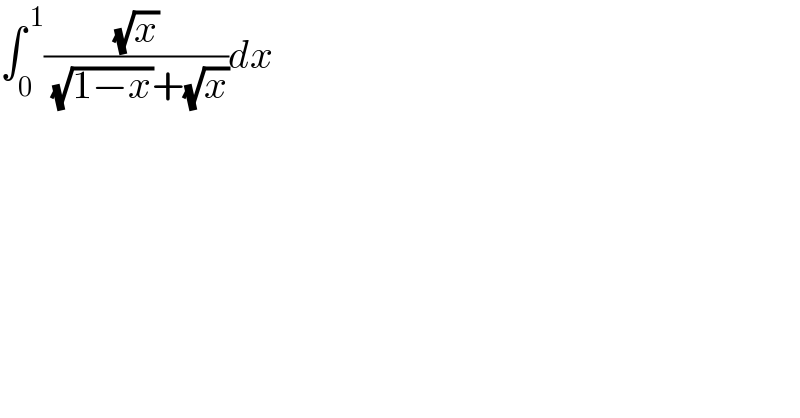
∫_0 ^( 1) ((√x)/( (√(1−x))+(√x)))dx
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx} \\ $$
Answered by qaz last updated on 25/Apr/21
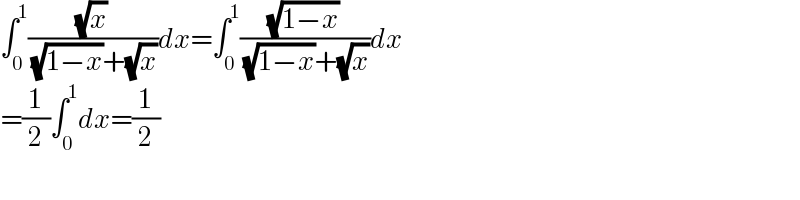
∫_0 ^1 ((√x)/( (√(1−x))+(√x)))dx=∫_0 ^1 ((√(1−x))/( (√(1−x))+(√x)))dx =(1/2)∫_0 ^1 dx=(1/2)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {dx}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mohammad17 last updated on 25/Apr/21
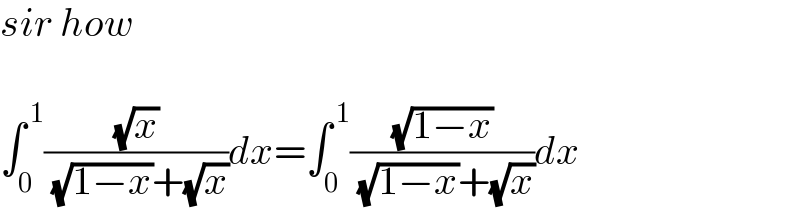
sir how ∫_0 ^( 1) ((√x)/( (√(1−x))+(√x)))dx=∫_0 ^( 1) ((√(1−x))/( (√(1−x))+(√x)))dx
$${sir}\:{how} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx} \\ $$
Commented by Ar Brandon last updated on 25/Apr/21
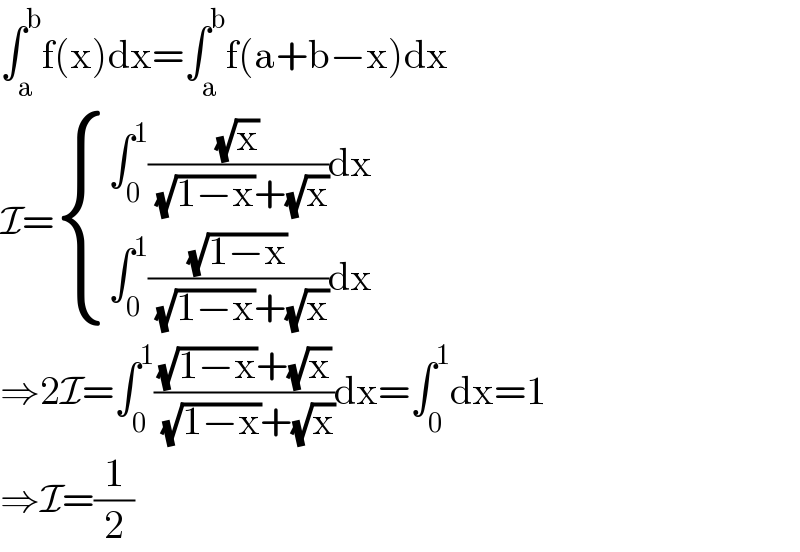
∫_a ^b f(x)dx=∫_a ^b f(a+b−x)dx I= { ((∫_0 ^1 ((√x)/( (√(1−x))+(√x)))dx)),((∫_0 ^1 ((√(1−x))/( (√(1−x))+(√x)))dx)) :} ⇒2I=∫_0 ^1 (((√(1−x))+(√x))/( (√(1−x))+(√x)))dx=∫_0 ^1 dx=1 ⇒I=(1/2)
$$\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathcal{I}=\begin{cases}{\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}}\\{\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}}\end{cases} \\ $$$$\Rightarrow\mathrm{2}\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{dx}=\mathrm{1} \\ $$$$\Rightarrow\mathcal{I}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 25/Apr/21
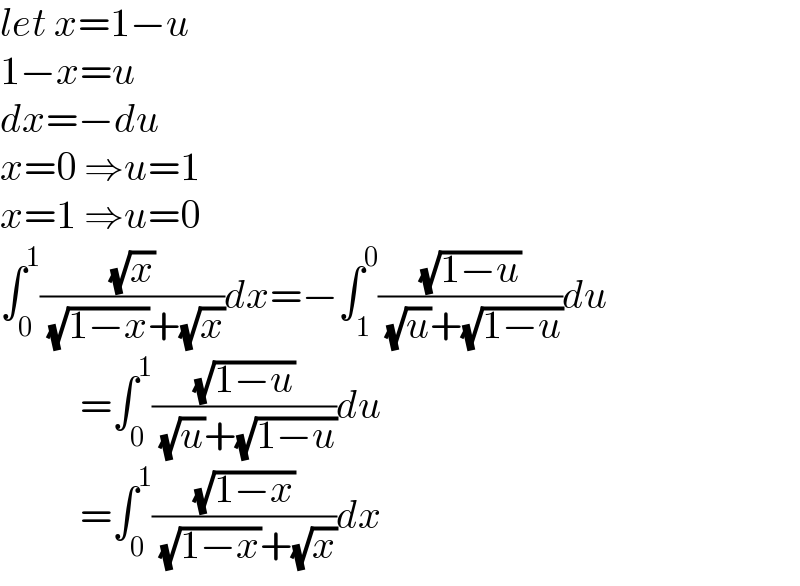
let x=1−u 1−x=u dx=−du x=0 ⇒u=1 x=1 ⇒u=0 ∫_0 ^1 ((√x)/( (√(1−x))+(√x)))dx=−∫_1 ^0 ((√(1−u))/( (√u)+(√(1−u))))du =∫_0 ^1 ((√(1−u))/( (√u)+(√(1−u))))du =∫_0 ^1 ((√(1−x))/( (√(1−x))+(√x)))dx
$${let}\:{x}=\mathrm{1}−{u} \\ $$$$\mathrm{1}−{x}={u} \\ $$$${dx}=−{du} \\ $$$${x}=\mathrm{0}\:\Rightarrow{u}=\mathrm{1} \\ $$$${x}=\mathrm{1}\:\Rightarrow{u}=\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx}=−\int_{\mathrm{1}} ^{\mathrm{0}} \frac{\sqrt{\mathrm{1}−{u}}}{\:\sqrt{{u}}+\sqrt{\mathrm{1}−{u}}}{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−{u}}}{\:\sqrt{{u}}+\sqrt{\mathrm{1}−{u}}}{du} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx} \\ $$
Answered by Mathspace last updated on 25/Apr/21
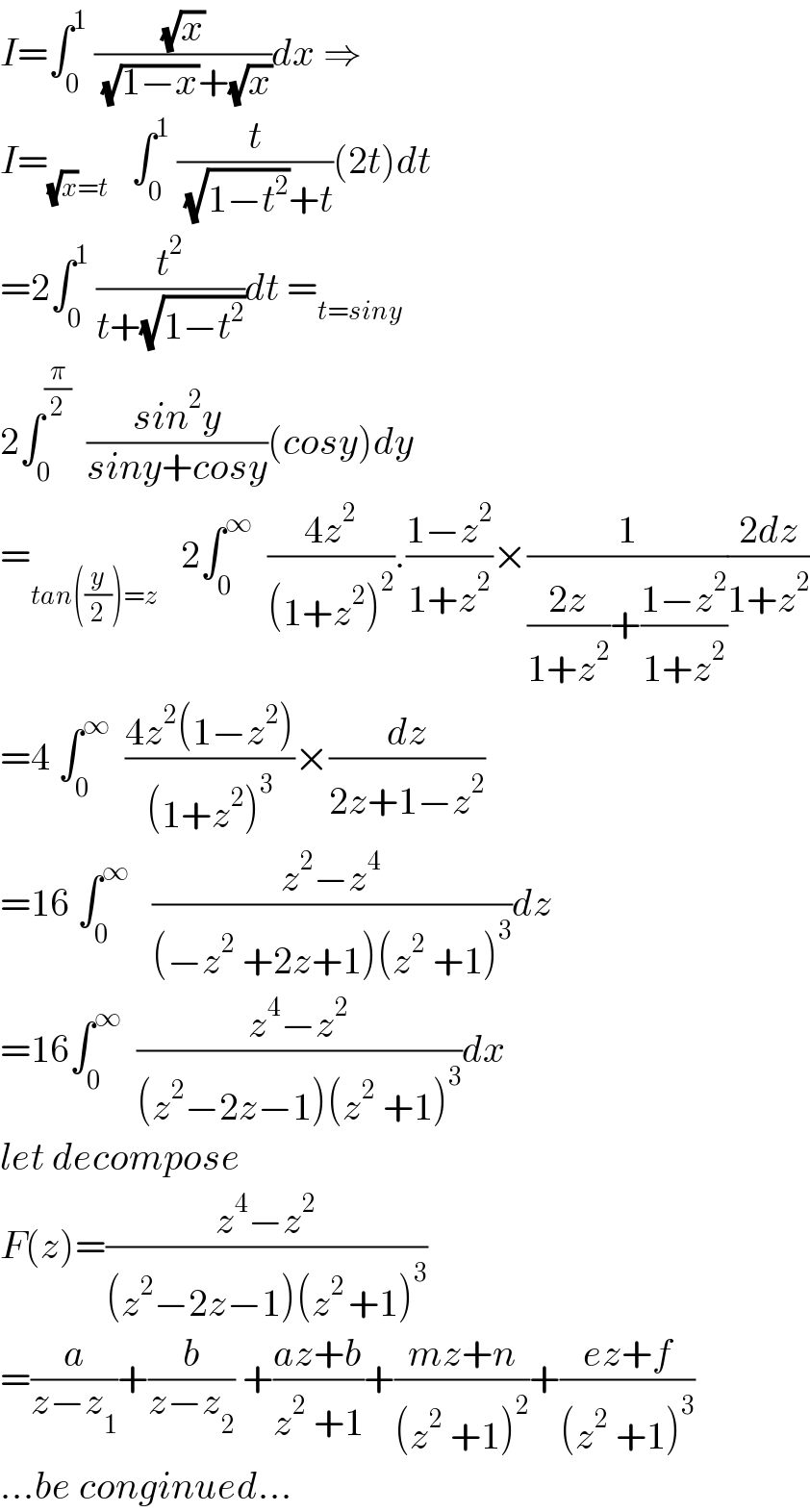
I=∫_0 ^1 ((√x)/( (√(1−x))+(√x)))dx ⇒ I=_((√x)=t) ∫_0 ^1 (t/( (√(1−t^2 ))+t))(2t)dt =2∫_0 ^1 (t^2 /(t+(√(1−t^2 ))))dt =_(t=siny) 2∫_0 ^(π/2) ((sin^2 y)/(siny+cosy))(cosy)dy =_(tan((y/2))=z) 2∫_0 ^∞ ((4z^2 )/((1+z^2 )^2 )).((1−z^2 )/(1+z^2 ))×(1/(((2z)/(1+z^2 ))+((1−z^2 )/(1+z^2 ))))((2dz)/(1+z^2 )) =4 ∫_0 ^∞ ((4z^2 (1−z^2 ))/((1+z^2 )^3 ))×(dz/(2z+1−z^2 )) =16 ∫_0 ^∞ ((z^2 −z^4 )/((−z^2 +2z+1)(z^2 +1)^3 ))dz =16∫_0 ^∞ ((z^4 −z^2 )/((z^2 −2z−1)(z^2 +1)^3 ))dx let decompose F(z)=((z^4 −z^2 )/((z^2 −2z−1)(z^(2 ) +1)^3 )) =(a/(z−z_1 ))+(b/(z−z_2 )) +((az+b)/(z^2 +1))+((mz+n)/((z^2 +1)^2 ))+((ez+f)/((z^2 +1)^3 )) ...be conginued...
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx}\:\Rightarrow \\ $$$${I}=_{\sqrt{{x}}={t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }+{t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{t}^{\mathrm{2}} }{{t}+\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}\:=_{{t}={siny}} \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{sin}^{\mathrm{2}} {y}}{{siny}+{cosy}}\left({cosy}\right){dy} \\ $$$$=_{{tan}\left(\frac{{y}}{\mathrm{2}}\right)={z}} \:\:\:\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{4}{z}^{\mathrm{2}} }{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)^{\mathrm{2}} }.\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }×\frac{\mathrm{1}}{\frac{\mathrm{2}{z}}{\mathrm{1}+{z}^{\mathrm{2}} }+\frac{\mathrm{1}−{z}^{\mathrm{2}} }{\mathrm{1}+{z}^{\mathrm{2}} }}\frac{\mathrm{2}{dz}}{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{4}{z}^{\mathrm{2}} \left(\mathrm{1}−{z}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{z}^{\mathrm{2}} \right)^{\mathrm{3}} }×\frac{{dz}}{\mathrm{2}{z}+\mathrm{1}−{z}^{\mathrm{2}} } \\ $$$$=\mathrm{16}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{z}^{\mathrm{2}} −{z}^{\mathrm{4}} }{\left(−{z}^{\mathrm{2}} \:+\mathrm{2}{z}+\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }{dz} \\ $$$$=\mathrm{16}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{1}\right)\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$$${let}\:{decompose} \\ $$$${F}\left({z}\right)=\frac{{z}^{\mathrm{4}} −{z}^{\mathrm{2}} }{\left({z}^{\mathrm{2}} −\mathrm{2}{z}−\mathrm{1}\right)\left({z}^{\mathrm{2}\:} +\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$=\frac{{a}}{{z}−{z}_{\mathrm{1}} }+\frac{{b}}{{z}−{z}_{\mathrm{2}} }\:+\frac{{az}+{b}}{{z}^{\mathrm{2}} \:+\mathrm{1}}+\frac{{mz}+{n}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{ez}+{f}}{\left({z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} } \\ $$$$…{be}\:{conginued}… \\ $$
Answered by MJS_new last updated on 25/Apr/21
∫((√x)/( (√(1−x))+(√x)))dx= [t=((√(1−x))/( (√x))) → dx=−2(√(1−x))(√x^3 )dt; x=(1/(t^2 +1))] =−2∫(t/((t+1)(t^2 +1)^2 ))dt= =(1/2)∫(((t^2 −2t−1)/((t^2 +1)^2 ))−(t/(t^2 +1))+(1/(t+1)))dt= ... =−((t−1)/(2(t^2 +1)))−(1/4)ln (t^2 +1) +(1/2)ln (t+1) = =−((t−1)/(2(t^2 +1)))+(1/4)ln (((t+1)^2 )/(t^2 +1)) = =((x−(√((1−x)x))+ln ((√(1−x))+(√x)))/2)+C
$$\int\frac{\sqrt{{x}}}{\:\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{1}−{x}}}{\:\sqrt{{x}}}\:\rightarrow\:{dx}=−\mathrm{2}\sqrt{\mathrm{1}−{x}}\sqrt{{x}^{\mathrm{3}} }{dt};\:{x}=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=−\mathrm{2}\int\frac{{t}}{\left({t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}= \\ $$$$… \\ $$$$=−\frac{{t}−\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\left({t}^{\mathrm{2}} +\mathrm{1}\right)\:+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}+\mathrm{1}\right)\:= \\ $$$$=−\frac{{t}−\mathrm{1}}{\mathrm{2}\left({t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{ln}\:\frac{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{1}}\:= \\ $$$$=\frac{{x}−\sqrt{\left(\mathrm{1}−{x}\right){x}}+\mathrm{ln}\:\left(\sqrt{\mathrm{1}−{x}}+\sqrt{{x}}\right)}{\mathrm{2}}+{C} \\ $$
Answered by mathmax by abdo last updated on 26/Apr/21
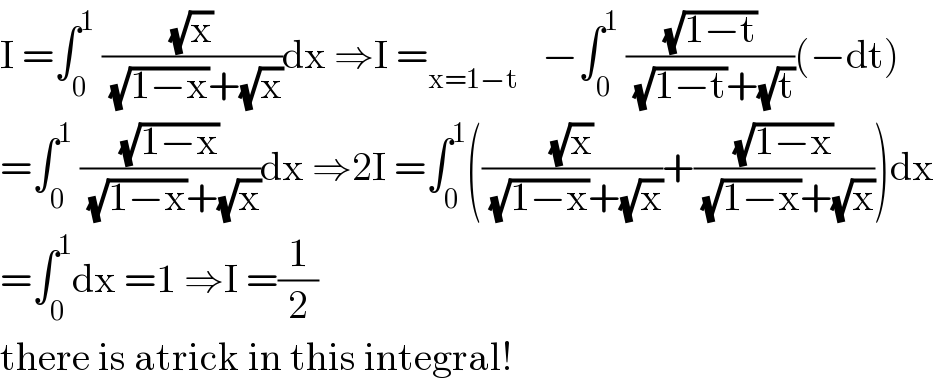
I =∫_0 ^1 ((√x)/( (√(1−x))+(√x)))dx ⇒I =_(x=1−t) −∫_0 ^1 ((√(1−t))/( (√(1−t))+(√t)))(−dt) =∫_0 ^1 ((√(1−x))/( (√(1−x))+(√x)))dx ⇒2I =∫_0 ^1 (((√x)/( (√(1−x))+(√x)))+((√(1−x))/( (√(1−x))+(√x))))dx =∫_0 ^1 dx =1 ⇒I =(1/2) there is atrick in this integral!
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=_{\mathrm{x}=\mathrm{1}−\mathrm{t}} \:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\mathrm{t}}}{\:\sqrt{\mathrm{1}−\mathrm{t}}+\sqrt{\mathrm{t}}}\left(−\mathrm{dt}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\mathrm{dx}\:\Rightarrow\mathrm{2I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\sqrt{\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}+\frac{\sqrt{\mathrm{1}−\mathrm{x}}}{\:\sqrt{\mathrm{1}−\mathrm{x}}+\sqrt{\mathrm{x}}}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{dx}\:=\mathrm{1}\:\Rightarrow\mathrm{I}\:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{there}\:\mathrm{is}\:\mathrm{atrick}\:\mathrm{in}\:\mathrm{this}\:\mathrm{integral}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *