Question Number 133591 by benjo_mathlover last updated on 23/Feb/21
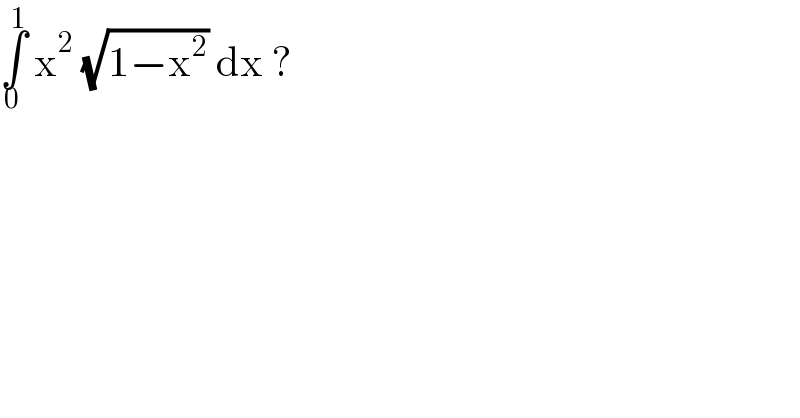
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{2}} \:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:?\: \\ $$
Answered by EDWIN88 last updated on 23/Feb/21
![by Ostrogradsky method ∫ x^2 (√(1−x^2 )) dx = (ax^3 +bx^2 +cx+d)(√(1−x^2 )) +∫ (e/( (√(1−x^2 )))) dx differentiating both sides give x^2 (√(1−x^2 )) = (d/dx)(ax^3 +bx^2 +cx+d)(√(1−x^2 )) +(e/( (√(1−x^2 )))) x^2 (√(1−x^2 )) =(3ax^2 +2bx+c)(√(1−x^2 )) −((x(ax^3 +bx^2 +cx+x))/( (√(1−x^2 ))))+(e/( (√(1−x^2 )))) after solving for coefficient we get a=(1/4) ; b=0 ; c=−(1/8) ; d=0 ; e=(1/8) then ∫x^2 (√(1−x^2 )) dx = ((1/4)x^3 −(1/8)x)(√(1−x^2 )) +∫ (1/(8(√(1−x^2 )))) dx or ∫_0 ^( 1) x^2 (√(1−x^2 )) dx = [((1/4)x^3 −(1/( 8))x)(√(1−x^2 )) +(1/8)arcsin (x) ]_0 ^1 = (π/(16))](https://www.tinkutara.com/question/Q133592.png)
$$\mathrm{by}\:\mathrm{Ostrogradsky}\:\mathrm{method} \\ $$$$\int\:{x}^{\mathrm{2}} \:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:=\:\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\int\:\frac{\mathrm{e}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx} \\ $$$$\mathrm{differentiating}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{give}\: \\ $$$${x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\:\frac{{d}}{{dx}}\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{d}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\frac{{e}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$${x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:=\left(\mathrm{3}{ax}^{\mathrm{2}} +\mathrm{2}{bx}+{c}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:−\frac{{x}\left({ax}^{\mathrm{3}} +{bx}^{\mathrm{2}} +{cx}+{x}\right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}+\frac{{e}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{after}\:\mathrm{solving}\:\mathrm{for}\:\mathrm{coefficient}\:\mathrm{we}\:\mathrm{get}\: \\ $$$${a}=\frac{\mathrm{1}}{\mathrm{4}}\:;\:\mathrm{b}=\mathrm{0}\:;\:{c}=−\frac{\mathrm{1}}{\mathrm{8}}\:;\:\mathrm{d}=\mathrm{0}\:;\:\mathrm{e}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{then}\:\int{x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:=\:\left(\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{8}}{x}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\int\:\frac{\mathrm{1}}{\mathrm{8}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:{dx} \\ $$$${or}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:=\:\left[\left(\frac{\mathrm{1}}{\mathrm{4}}{x}^{\mathrm{3}} −\frac{\mathrm{1}}{\:\mathrm{8}}{x}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{arcsin}\:\left({x}\right)\:\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:=\:\frac{\pi}{\mathrm{16}}\: \\ $$
Commented by benjo_mathlover last updated on 23/Feb/21

$$\mathrm{amazing} \\ $$
Answered by Ñï= last updated on 23/Feb/21

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \sqrt{\mathrm{1}−{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {sin}^{\mathrm{2}} \theta{cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{3}\right)}=\frac{\mathrm{1}}{\mathrm{16}}\pi \\ $$
Answered by SEKRET last updated on 23/Feb/21
![∫_0 ^( 1) x^2 ∙(√(1−x^2 )) dx [((x=sin(t) /_0 ^1 →/_0 ^(𝛑/2) )),((dx= cos(t)dt )) ] ∫_0 ^(𝛑/2) sin^2 (x)∙cos^2 (t) dt=(1/4)∫_0 ^(𝛑/2) sin^2 (2t) dt (1/4)((1/2)t − ((sin(4t))/8)) /_0 ^( (𝛑/2)) = (𝛑/(16)) ABDULAZIZ ABDUVALIYEV](https://www.tinkutara.com/question/Q133598.png)
$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \boldsymbol{\mathrm{x}}^{\mathrm{2}} \centerdot\sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\:\:\boldsymbol{\mathrm{dx}}\:\:\begin{bmatrix}{\boldsymbol{\mathrm{x}}=\boldsymbol{\mathrm{sin}}\left(\boldsymbol{\mathrm{t}}\right)\:\:/_{\mathrm{0}} ^{\mathrm{1}} \rightarrow/_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\:}\\{\boldsymbol{\mathrm{dx}}=\:\boldsymbol{\mathrm{cos}}\left(\boldsymbol{\mathrm{t}}\right)\boldsymbol{\mathrm{dt}}\:}\end{bmatrix} \\ $$$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \:\boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{x}}\right)\centerdot\boldsymbol{\mathrm{cos}}^{\mathrm{2}} \left(\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}}=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \boldsymbol{\mathrm{sin}}^{\mathrm{2}} \left(\mathrm{2}\boldsymbol{\mathrm{t}}\right)\:\boldsymbol{\mathrm{dt}} \\ $$$$\:\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\mathrm{t}}\:−\:\frac{\boldsymbol{\mathrm{sin}}\left(\mathrm{4}\boldsymbol{\mathrm{t}}\right)}{\mathrm{8}}\right)\:/_{\mathrm{0}} ^{\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} =\:\frac{\boldsymbol{\pi}}{\mathrm{16}} \\ $$$$\:\:\boldsymbol{{ABDULAZIZ}}\:\:\boldsymbol{{ABDUVALIYEV}} \\ $$
Answered by benjo_mathlover last updated on 23/Feb/21

Answered by Dwaipayan Shikari last updated on 23/Feb/21
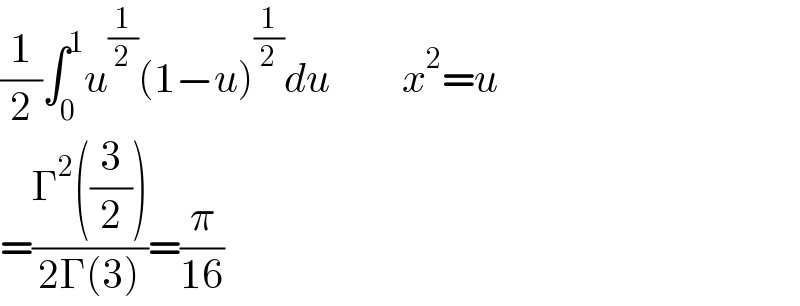
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {u}^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{1}−{u}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {du}\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} ={u} \\ $$$$=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}\Gamma\left(\mathrm{3}\right)}=\frac{\pi}{\mathrm{16}} \\ $$
Answered by mathmax by abdo last updated on 24/Feb/21
![I =∫_0 ^1 x^2 (√(1−x^2 ))dx changement x=sint give I =∫_0 ^(π/2) sin^2 t.cost.cost dt =∫_0 ^(π/2) (sint cost)^2 dt =(1/4)∫_0 ^(π/2) sin^2 (2t)dt =(1/8)∫_0 ^(π/2) (1−cos(4t))dt =(π/(16))−(1/(32))[sin(4t)]_0 ^(π/2) =(π/(16))−0 ⇒I=(π/(16))](https://www.tinkutara.com/question/Q133753.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sint}\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \mathrm{t}.\mathrm{cost}.\mathrm{cost}\:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{sint}\:\mathrm{cost}\right)^{\mathrm{2}} \mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{2}} \left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{4t}\right)\right)\mathrm{dt}\:=\frac{\pi}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{32}}\left[\mathrm{sin}\left(\mathrm{4t}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{16}}−\mathrm{0}\:\:\Rightarrow\mathrm{I}=\frac{\pi}{\mathrm{16}} \\ $$
