Question Number 133222 by john_santu last updated on 20/Feb/21
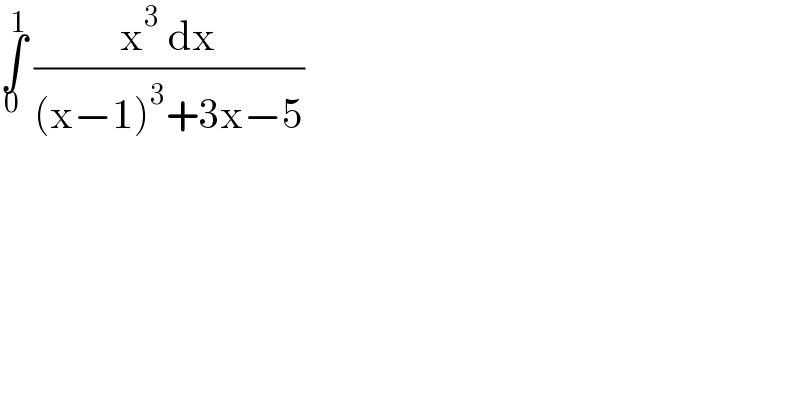
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{x}^{\mathrm{3}} \:\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}} \\ $$
Answered by liberty last updated on 20/Feb/21
![I = ∫_0 ^1 ((x^3 dx)/((x−1)^3 +3x−5)) let x−1 = ℓ I=∫_(−1) ^0 (((ℓ+1)^3 )/(ℓ^3 +3ℓ−2)) dℓ I=∫_(−1) ^0 ((l^3 +3l^2 +3l+1)/(l^3 +3l−2)) dl I= ∫_(−1) ^0 (1+((3l^2 +3)/(l^3 +3l−2)))dl I=l ]_(−1) ^0 +∫_(−1) ^0 ((d(l^3 +3l−2))/(l^3 +3l−2)) I= 1+ln ∣l^3 +3l−2∣ ]_(−1) ^0 I=1+ln ∣2∣−ln ∣6∣ I=1+ln ((1/3))=1−ln (3)](https://www.tinkutara.com/question/Q133237.png)
$$\:\mathrm{I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{x}^{\mathrm{3}} \:\mathrm{dx}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} +\mathrm{3x}−\mathrm{5}} \\ $$$$\mathrm{let}\:\mathrm{x}−\mathrm{1}\:=\:\ell\: \\ $$$$\mathrm{I}=\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\:\frac{\left(\ell+\mathrm{1}\right)^{\mathrm{3}} }{\ell^{\mathrm{3}} +\mathrm{3}\ell−\mathrm{2}}\:\mathrm{d}\ell \\ $$$$\mathrm{I}=\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\:\frac{{l}^{\mathrm{3}} +\mathrm{3}{l}^{\mathrm{2}} +\mathrm{3}{l}+\mathrm{1}}{{l}^{\mathrm{3}} +\mathrm{3}{l}−\mathrm{2}}\:{dl} \\ $$$$\mathrm{I}=\:\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\:\left(\mathrm{1}+\frac{\mathrm{3}{l}^{\mathrm{2}} +\mathrm{3}}{{l}^{\mathrm{3}} +\mathrm{3}{l}−\mathrm{2}}\right){dl} \\ $$$$\left.\mathrm{I}={l}\:\right]_{−\mathrm{1}} ^{\mathrm{0}} +\underset{−\mathrm{1}} {\overset{\mathrm{0}} {\int}}\frac{\mathrm{d}\left({l}^{\mathrm{3}} +\mathrm{3}{l}−\mathrm{2}\right)}{{l}^{\mathrm{3}} +\mathrm{3}{l}−\mathrm{2}}\: \\ $$$$\left.\mathrm{I}=\:\mathrm{1}+\mathrm{ln}\:\mid{l}^{\mathrm{3}} +\mathrm{3}{l}−\mathrm{2}\mid\:\right]_{−\mathrm{1}} ^{\mathrm{0}} \\ $$$$\mathrm{I}=\mathrm{1}+\mathrm{ln}\:\mid\mathrm{2}\mid−\mathrm{ln}\:\mid\mathrm{6}\mid\: \\ $$$$\mathrm{I}=\mathrm{1}+\mathrm{ln}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{1}−\mathrm{ln}\:\left(\mathrm{3}\right) \\ $$
