Menu Close

0-1-x-3-ln-x-dx-1-x-3-e-x-1-dx-

Tinku Tara
Pin




Question Number 325 by 123456 last updated on 25/Jan/15
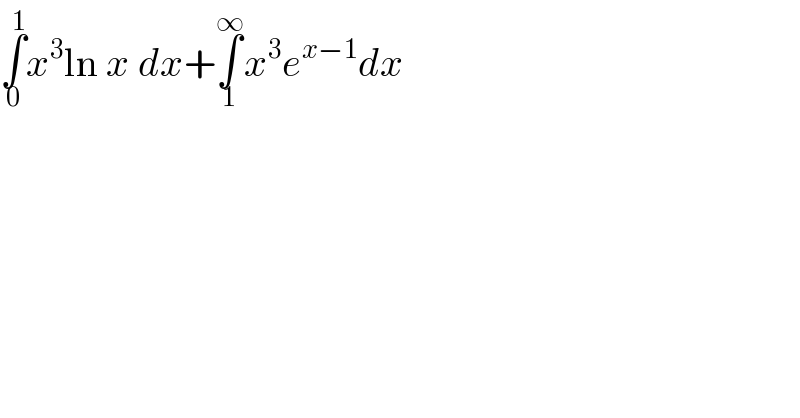
∫_0 ^1 x^3 ln x dx+∫_1 ^∞ x^3 e^(x−1) dx
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{3}} \mathrm{ln}\:{x}\:{dx}+\underset{\mathrm{1}} {\overset{\infty} {\int}}{x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} {dx} \\ $$
Answered by prakash jain last updated on 22/Dec/14
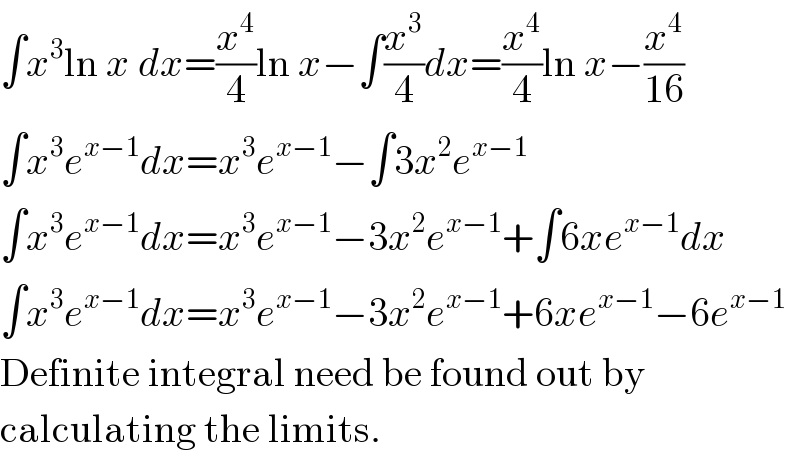
∫x^3 ln x dx=(x^4 /4)ln x−∫(x^3 /4)dx=(x^4 /4)ln x−(x^4 /(16)) ∫x^3 e^(x−1) dx=x^3 e^(x−1) −∫3x^2 e^(x−1) ∫x^3 e^(x−1) dx=x^3 e^(x−1) −3x^2 e^(x−1) +∫6xe^(x−1) dx ∫x^3 e^(x−1) dx=x^3 e^(x−1) −3x^2 e^(x−1) +6xe^(x−1) −6e^(x−1) Definite integral need be found out by calculating the limits.
$$\int{x}^{\mathrm{3}} \mathrm{ln}\:{x}\:{dx}=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\mathrm{ln}\:{x}−\int\frac{{x}^{\mathrm{3}} }{\mathrm{4}}{dx}=\frac{{x}^{\mathrm{4}} }{\mathrm{4}}\mathrm{ln}\:{x}−\frac{{x}^{\mathrm{4}} }{\mathrm{16}} \\ $$$$\int{x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} {dx}={x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} −\int\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}−\mathrm{1}} \\ $$$$\int{x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} {dx}={x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}−\mathrm{1}} +\int\mathrm{6}{xe}^{{x}−\mathrm{1}} {dx} \\ $$$$\int{x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} {dx}={x}^{\mathrm{3}} {e}^{{x}−\mathrm{1}} −\mathrm{3}{x}^{\mathrm{2}} {e}^{{x}−\mathrm{1}} +\mathrm{6}{xe}^{{x}−\mathrm{1}} −\mathrm{6}{e}^{{x}−\mathrm{1}} \\ $$$$\mathrm{Definite}\:\mathrm{integral}\:\mathrm{need}\:\mathrm{be}\:\mathrm{found}\:\mathrm{out}\:\mathrm{by} \\ $$$$\mathrm{calculating}\:\mathrm{the}\:\mathrm{limits}. \\ $$

Pin