Menu Close

0-1-x-4-x-2-1-3-dx-

Tinku Tara 0 Comments
Pin




Question Number 132089 by rs4089 last updated on 11/Feb/21
∫_0 ^∞ (1/((x^4 −x^2 +1)^3 ))dx
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }{dx} \\ $$
Answered by Lordose last updated on 11/Feb/21
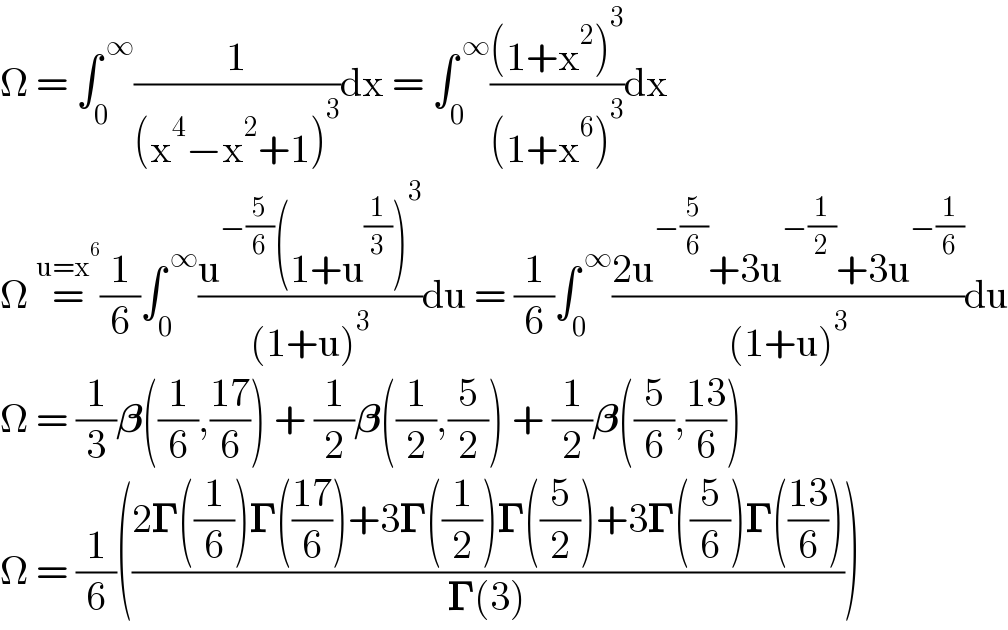
Ω = ∫_0 ^( ∞) (1/((x^4 −x^2 +1)^3 ))dx = ∫_0 ^( ∞) (((1+x^2 )^3 )/((1+x^6 )^3 ))dx Ω =^(u=x^6 ) (1/6)∫_0 ^( ∞) ((u^(−(5/6)) (1+u^(1/3) )^3 )/((1+u)^3 ))du = (1/6)∫_0 ^( ∞) ((2u^(−(5/6)) +3u^(−(1/2)) +3u^(−(1/6)) )/((1+u)^3 ))du Ω = (1/3)𝛃((1/6),((17)/6)) + (1/2)𝛃((1/2),(5/2)) + (1/2)𝛃((5/6),((13)/6)) Ω = (1/6)(((2𝚪((1/6))𝚪(((17)/6))+3𝚪((1/2))𝚪((5/2))+3𝚪((5/6))𝚪(((13)/6)))/(𝚪(3))))
$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{3}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{3}} }\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{u}=\mathrm{x}^{\mathrm{6}} } {=}\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{−\frac{\mathrm{5}}{\mathrm{6}}} \left(\mathrm{1}+\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}} \right)^{\mathrm{3}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{3}} }\mathrm{du}\:=\:\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2u}^{−\frac{\mathrm{5}}{\mathrm{6}}} +\mathrm{3u}^{−\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{3u}^{−\frac{\mathrm{1}}{\mathrm{6}}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{3}} }\mathrm{du} \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{3}}\boldsymbol{\beta}\left(\frac{\mathrm{1}}{\mathrm{6}},\frac{\mathrm{17}}{\mathrm{6}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\beta}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{5}}{\mathrm{2}}\right)\:+\:\frac{\mathrm{1}}{\mathrm{2}}\boldsymbol{\beta}\left(\frac{\mathrm{5}}{\mathrm{6}},\frac{\mathrm{13}}{\mathrm{6}}\right) \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\mathrm{2}\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{17}}{\mathrm{6}}\right)+\mathrm{3}\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{5}}{\mathrm{2}}\right)+\mathrm{3}\boldsymbol{\Gamma}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\boldsymbol{\Gamma}\left(\frac{\mathrm{13}}{\mathrm{6}}\right)}{\boldsymbol{\Gamma}\left(\mathrm{3}\right)}\right)\: \\ $$
Commented by Ar Brandon last updated on 11/Feb/21
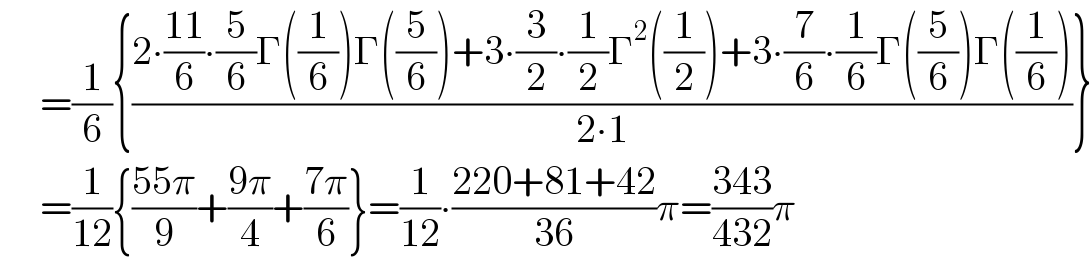
=(1/6){((2∙((11)/6)∙(5/6)Γ((1/6))Γ((5/6))+3∙(3/2)∙(1/2)Γ^2 ((1/2))+3∙(7/6)∙(1/6)Γ((5/6))Γ((1/6)))/(2∙1))} =(1/(12)){((55π)/9)+((9π)/4)+((7π)/6)}=(1/(12))∙((220+81+42)/(36))π=((343)/(432))π
$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{6}}\left\{\frac{\mathrm{2}\centerdot\frac{\mathrm{11}}{\mathrm{6}}\centerdot\frac{\mathrm{5}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)+\mathrm{3}\centerdot\frac{\mathrm{3}}{\mathrm{2}}\centerdot\frac{\mathrm{1}}{\mathrm{2}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{3}\centerdot\frac{\mathrm{7}}{\mathrm{6}}\centerdot\frac{\mathrm{1}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)}{\mathrm{2}\centerdot\mathrm{1}}\right\} \\ $$$$\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{12}}\left\{\frac{\mathrm{55}\pi}{\mathrm{9}}+\frac{\mathrm{9}\pi}{\mathrm{4}}+\frac{\mathrm{7}\pi}{\mathrm{6}}\right\}=\frac{\mathrm{1}}{\mathrm{12}}\centerdot\frac{\mathrm{220}+\mathrm{81}+\mathrm{42}}{\mathrm{36}}\pi=\frac{\mathrm{343}}{\mathrm{432}}\pi \\ $$
Commented by Lordose last updated on 11/Feb/21
Finishing touches, hahaha
$$\mathrm{Finishing}\:\mathrm{touches},\:\mathrm{hahaha} \\ $$
Commented by Ar Brandon last updated on 11/Feb/21
��

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *