Question Number 139811 by mnjuly1970 last updated on 01/May/21
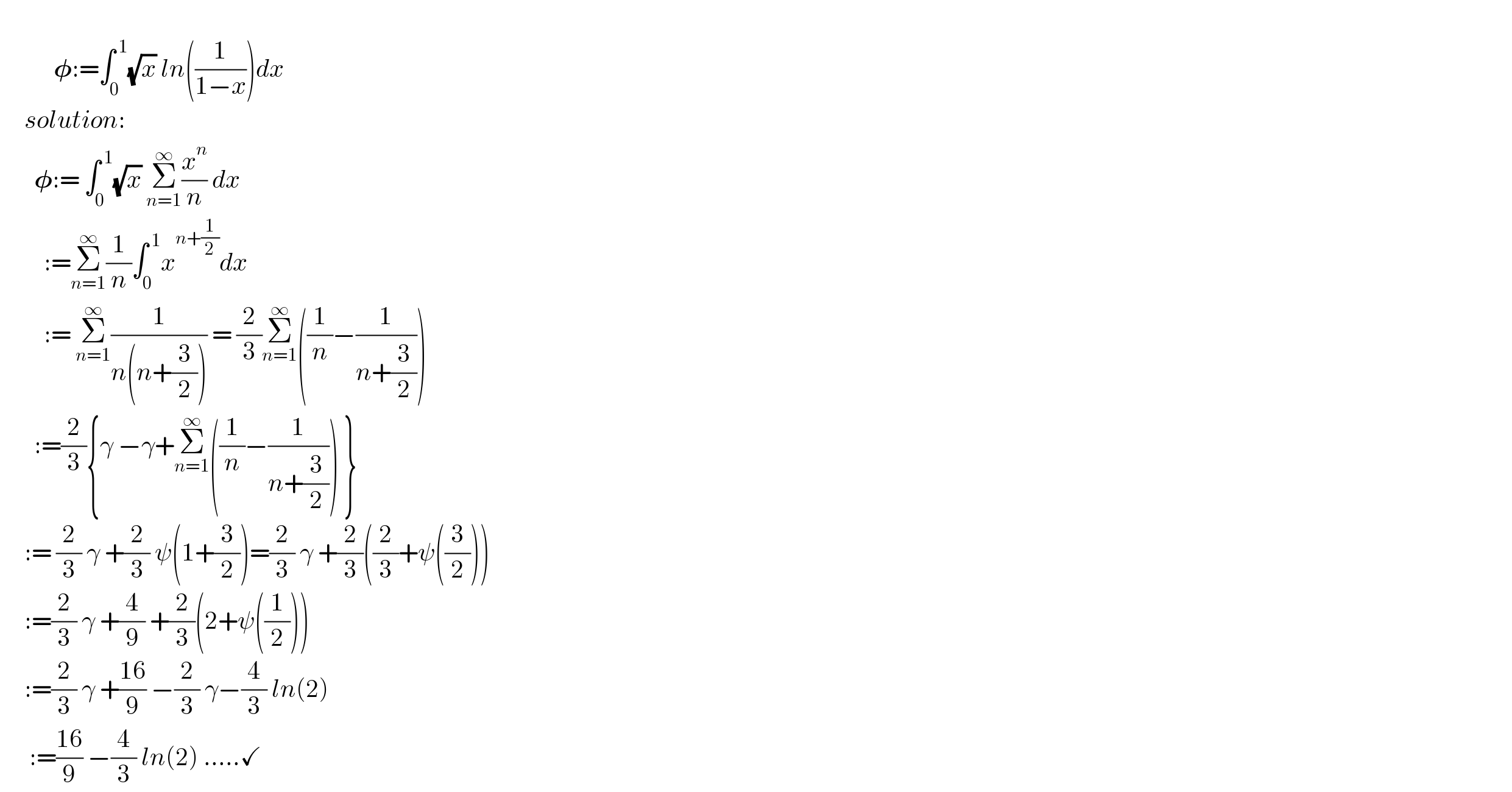
$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}:=\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{{x}}\:{ln}\left(\frac{\mathrm{1}}{\mathrm{1}−{x}}\right){dx} \\ $$$$\:\:\:\:\:{solution}: \\ $$$$\:\:\:\:\:\:\:\boldsymbol{\phi}:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \sqrt{{x}}\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\::=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\:\mathrm{1}} {x}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\::=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\left({n}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:=\:\frac{\mathrm{2}}{\mathrm{3}}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}}{\mathrm{2}}}\right) \\ $$$$\:\:\:\:\:\:\::=\frac{\mathrm{2}}{\mathrm{3}}\left\{\gamma\:−\gamma+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\frac{\mathrm{3}}{\mathrm{2}}}\right)\:\right\} \\ $$$$\:\:\:\:\::=\:\frac{\mathrm{2}}{\mathrm{3}}\:\gamma\:+\frac{\mathrm{2}}{\mathrm{3}}\:\psi\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\mathrm{2}}{\mathrm{3}}\:\gamma\:+\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{2}}{\mathrm{3}}+\psi\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\::=\frac{\mathrm{2}}{\mathrm{3}}\:\gamma\:+\frac{\mathrm{4}}{\mathrm{9}}\:+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2}+\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$$$\:\:\:\:\::=\frac{\mathrm{2}}{\mathrm{3}}\:\gamma\:+\frac{\mathrm{16}}{\mathrm{9}}\:−\frac{\mathrm{2}}{\mathrm{3}}\:\gamma−\frac{\mathrm{4}}{\mathrm{3}}\:{ln}\left(\mathrm{2}\right)\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\::=\frac{\mathrm{16}}{\mathrm{9}}\:−\frac{\mathrm{4}}{\mathrm{3}}\:{ln}\left(\mathrm{2}\right)\:…..\checkmark\:\: \\ $$
Answered by mathmax by abdo last updated on 01/May/21
![Φ=∫_0 ^1 (√x)log((1/(1−x)))dx ⇒Φ=−∫_0 ^1 (√x)log(1−x)dx =_((√x)=t) −∫_0 ^1 t log(1−t^2 )(2t)dt =−2∫_0 ^1 t^2 log(1−t^2 )dt =−2{ [((t^3 −1)/3)log(1−t^2 )]_0 ^1 −∫_0 ^1 ((t^3 −1)/3)×((−2t)/(1−t^2 ))dt} =−(4/3) ∫_0 ^1 ((t^4 −t)/(1−t^2 ))dt =(4/3)∫_0 ^1 ((t(t^3 −1))/((t−1)(t+1)))dt =(4/3) ∫_0 ^1 ((t(t^2 +t+1))/(t+1))dt =(4/3)∫_0 ^1 ((t^3 +t^2 +t)/(t+1))dt =_(t+1=y) (4/3)∫_1 ^2 (((y−1)^3 +(y−1)^2 +y−1)/y)dy =(4/3)∫_1 ^2 ((y^3 −3y^2 +3y−1+y^2 −2y+1+y−1)/y)dy =(4/3)∫_1 ^2 ((y^3 −2y^2 +2y−1)/y)dy =(4/3)∫_1 ^2 (y^2 −2y+2−(1/y))dy =(4/3)[(y^3 /3)−y^2 +2y−log∣y∣]_1 ^2 =(4/3){(8/3)−4+4−log2−(1/3)+1−2} =(4/3){(7/3)−1−log2} =(4/3)((4/3)−log2) =((16)/9)−(4/3)log2](https://www.tinkutara.com/question/Q139827.png)
$$\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{x}}\mathrm{log}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\mathrm{dx}\:\Rightarrow\Phi=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\mathrm{x}}\mathrm{log}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$=_{\sqrt{\mathrm{x}}=\mathrm{t}} \:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{t}\:\mathrm{log}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{2t}\right)\mathrm{dt} \\ $$$$=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{2}} \:\mathrm{log}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{dt} \\ $$$$=−\mathrm{2}\left\{\:\:\left[\frac{\mathrm{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{3}}\mathrm{log}\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}^{\mathrm{3}} −\mathrm{1}}{\mathrm{3}}×\frac{−\mathrm{2t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\right\} \\ $$$$=−\frac{\mathrm{4}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{t}^{\mathrm{4}} −\mathrm{t}}{\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:\:=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}\left(\mathrm{t}^{\mathrm{3}} −\mathrm{1}\right)}{\left(\mathrm{t}−\mathrm{1}\right)\left(\mathrm{t}+\mathrm{1}\right)}\mathrm{dt} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{t}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{t}+\mathrm{1}\right)}{\mathrm{t}+\mathrm{1}}\mathrm{dt}\:=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{t}^{\mathrm{3}} \:+\mathrm{t}^{\mathrm{2}} \:+\mathrm{t}}{\mathrm{t}+\mathrm{1}}\mathrm{dt} \\ $$$$=_{\mathrm{t}+\mathrm{1}=\mathrm{y}} \:\:\:\:\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{3}} \:+\left(\mathrm{y}−\mathrm{1}\right)^{\mathrm{2}} \:+\mathrm{y}−\mathrm{1}}{\mathrm{y}}\mathrm{dy} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{y}^{\mathrm{3}} −\mathrm{3y}^{\mathrm{2}} \:+\mathrm{3y}−\mathrm{1}+\mathrm{y}^{\mathrm{2}} −\mathrm{2y}+\mathrm{1}+\mathrm{y}−\mathrm{1}}{\mathrm{y}}\mathrm{dy} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{1}} ^{\mathrm{2}} \:\frac{\mathrm{y}^{\mathrm{3}} −\mathrm{2y}^{\mathrm{2}} +\mathrm{2y}−\mathrm{1}}{\mathrm{y}}\mathrm{dy} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\int_{\mathrm{1}} ^{\mathrm{2}} \left(\mathrm{y}^{\mathrm{2}} −\mathrm{2y}+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{y}}\right)\mathrm{dy} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left[\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{y}^{\mathrm{2}} \:+\mathrm{2y}−\mathrm{log}\mid\mathrm{y}\mid\right]_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left\{\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{4}+\mathrm{4}−\mathrm{log2}−\frac{\mathrm{1}}{\mathrm{3}}+\mathrm{1}−\mathrm{2}\right\} \\ $$$$=\frac{\mathrm{4}}{\mathrm{3}}\left\{\frac{\mathrm{7}}{\mathrm{3}}−\mathrm{1}−\mathrm{log2}\right\}\:=\frac{\mathrm{4}}{\mathrm{3}}\left(\frac{\mathrm{4}}{\mathrm{3}}−\mathrm{log2}\right)\:=\frac{\mathrm{16}}{\mathrm{9}}−\frac{\mathrm{4}}{\mathrm{3}}\mathrm{log2} \\ $$
Commented by mnjuly1970 last updated on 01/May/21

$${thx}\:{sir}\:{max}\:… \\ $$
Commented by mathmax by abdo last updated on 02/May/21

$$\mathrm{you}\:\mathrm{are}\:\mathrm{welcome}\:\mathrm{sir} \\ $$
Answered by Ar Brandon last updated on 16/May/21
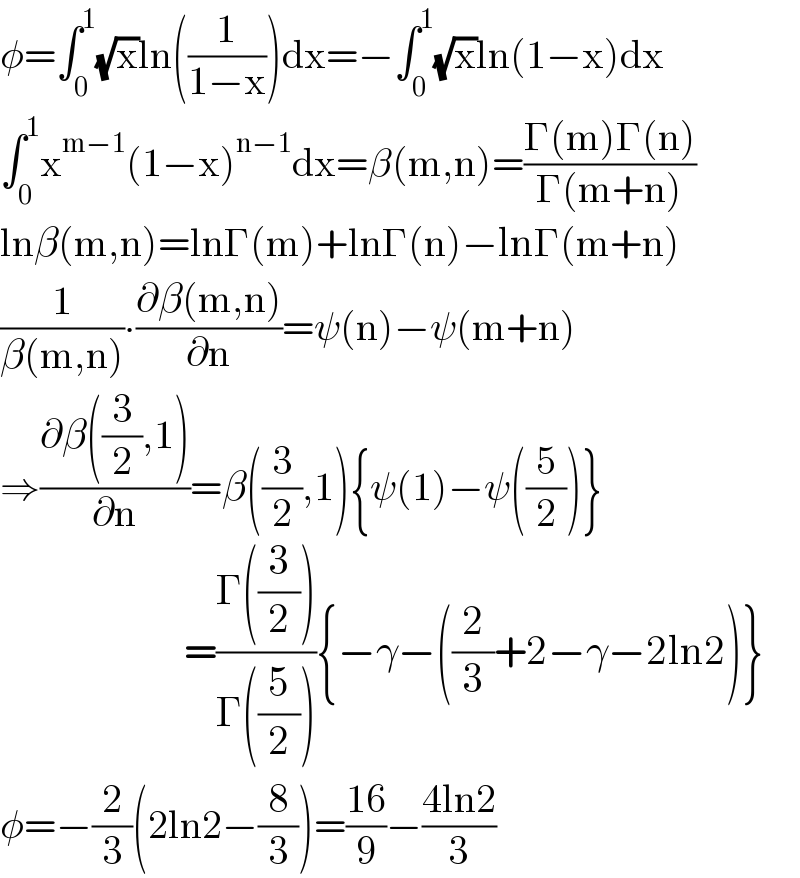
$$\phi=\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}}\mathrm{ln}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\mathrm{dx}=−\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{x}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{m}−\mathrm{1}} \left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{dx}=\beta\left(\mathrm{m},\mathrm{n}\right)=\frac{\Gamma\left(\mathrm{m}\right)\Gamma\left(\mathrm{n}\right)}{\Gamma\left(\mathrm{m}+\mathrm{n}\right)} \\ $$$$\mathrm{ln}\beta\left(\mathrm{m},\mathrm{n}\right)=\mathrm{ln}\Gamma\left(\mathrm{m}\right)+\mathrm{ln}\Gamma\left(\mathrm{n}\right)−\mathrm{ln}\Gamma\left(\mathrm{m}+\mathrm{n}\right) \\ $$$$\frac{\mathrm{1}}{\beta\left(\mathrm{m},\mathrm{n}\right)}\centerdot\frac{\partial\beta\left(\mathrm{m},\mathrm{n}\right)}{\partial\mathrm{n}}=\psi\left(\mathrm{n}\right)−\psi\left(\mathrm{m}+\mathrm{n}\right) \\ $$$$\Rightarrow\frac{\partial\beta\left(\frac{\mathrm{3}}{\mathrm{2}},\mathrm{1}\right)}{\partial\mathrm{n}}=\beta\left(\frac{\mathrm{3}}{\mathrm{2}},\mathrm{1}\right)\left\{\psi\left(\mathrm{1}\right)−\psi\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)}\left\{−\gamma−\left(\frac{\mathrm{2}}{\mathrm{3}}+\mathrm{2}−\gamma−\mathrm{2ln2}\right)\right\} \\ $$$$\phi=−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{2ln2}−\frac{\mathrm{8}}{\mathrm{3}}\right)=\frac{\mathrm{16}}{\mathrm{9}}−\frac{\mathrm{4ln2}}{\mathrm{3}} \\ $$
Commented by mnjuly1970 last updated on 01/May/21
$$\:\:{grateful}\:{mr}\:{brandon}… \\ $$
Commented by SLVR last updated on 01/May/21
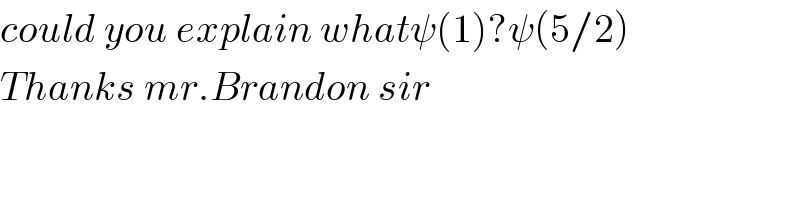
$${could}\:{you}\:{explain}\:{what}\psi\left(\mathrm{1}\right)?\psi\left(\mathrm{5}/\mathrm{2}\right) \\ $$$${Thanks}\:{mr}.{Brandon}\:{sir} \\ $$
Commented by Ar Brandon last updated on 01/May/21
$$\mathrm{You}'\mathrm{re}\:\mathrm{welcome}\:\mathrm{Sir} \\ $$
Commented by Ar Brandon last updated on 01/May/21

$$\Gamma'\left(\mathrm{x}\right)=\Gamma\left(\mathrm{x}\right)\psi\left(\mathrm{x}\right)\Rightarrow\frac{\Gamma'\left(\mathrm{x}\right)}{\Gamma\left(\mathrm{x}\right)}=\psi\left(\mathrm{x}\right) \\ $$$$\psi\left(\mathrm{s}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{s}}+\psi\left(\mathrm{s}\right)\:,\:\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=−\gamma−\mathrm{2ln2} \\ $$$$\psi\left(\mathrm{x}\right)=−\gamma+\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{x}}\right)\:\Rightarrow\psi\left(\mathrm{1}\right)=−\gamma \\ $$$$\psi\left(\mathrm{x}\right)\:\mathrm{represents}\:\mathrm{digamma}\:\mathrm{function}. \\ $$
Commented by SLVR last updated on 01/May/21
$${So}….{kind}\:{you}..{sir}\:\:{Great}…{explanation} \\ $$$${God}…{bless}\:{you}\:{for}\:{ever} \\ $$
Commented by Ar Brandon last updated on 01/May/21

$$\mathrm{Thanks}! \\ $$
