Question Number 142276 by mohammad17 last updated on 29/May/21
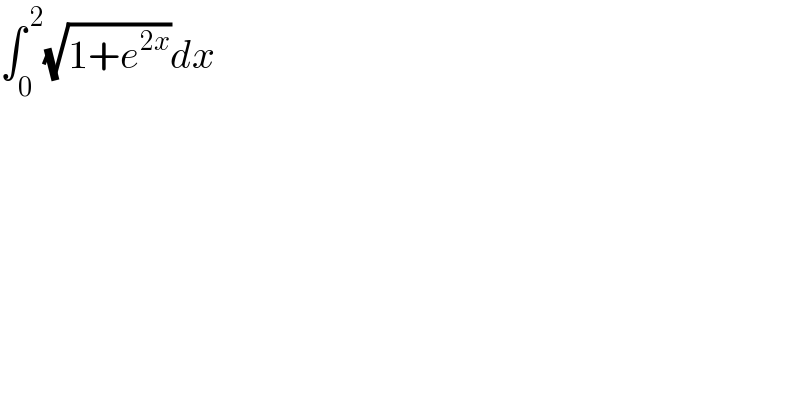
$$\int_{\mathrm{0}} ^{\:\mathrm{2}} \sqrt{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 29/May/21
![I∫_1 ^2 (√(1+e^(2x) )) dx changement e^(2x) =t give 2x=logt ⇒x=(1/2)logt ⇒ I=∫_e^2 ^e^4 (√(1+t))(dt/(2t)) =(1/2)∫_e^2 ^e^4 ((√(1+t))/t)dt =_((√(1+t))=y) (1/2)∫_(√(1+e^2 )) ^(√(1+e^4 )) (y/(y^2 −1))(2y)dy =∫_(√(1+e^2 )) ^(√(1+e^4 )) ((y^2 −1+1)/(y^2 −1))dy =∫_(√(1+e^2 )) ^(√(1+e^4 )) dy +∫_(√(1+e^2 )) ^(√(1+e^4 )) (dy/((y−1)(y+1))) =(√(1+e^4 ))−(√(1+e^2 )) +(1/2)∫_(√(1+e^2 )) ^(√(1+e^4 )) ((1/(y−1))−(1/(y+1)))dy =(√(1+e^4 ))−(√(1+e^2 )) +(1/2)[log∣((y−1)/(y+1))∣]_(√(1+e^2 )) ^(√(1+e^4 )) =(√(1+e^4 ))−(√(1+e^2 ))+(1/2){log∣(((√(1+e^4 ))−1)/( (√(1+e^4 +1))))∣−log∣(((√(1+e^2 ))−1)/( (√(1+e^2 ))+1))∣}](https://www.tinkutara.com/question/Q142294.png)
$$\mathrm{I}\int_{\mathrm{1}} ^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2x}} }\:\mathrm{dx}\:\mathrm{changement}\:\mathrm{e}^{\mathrm{2x}} \:=\mathrm{t}\:\mathrm{give}\:\mathrm{2x}=\mathrm{logt}\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{logt}\:\Rightarrow \\ $$$$\mathrm{I}=\int_{\mathrm{e}^{\mathrm{2}} } ^{\mathrm{e}^{\mathrm{4}} } \sqrt{\mathrm{1}+\mathrm{t}}\frac{\mathrm{dt}}{\mathrm{2t}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{e}^{\mathrm{2}} } ^{\mathrm{e}^{\mathrm{4}} } \:\:\frac{\sqrt{\mathrm{1}+\mathrm{t}}}{\mathrm{t}}\mathrm{dt}\:=_{\sqrt{\mathrm{1}+\mathrm{t}}=\mathrm{y}} \:\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \:\:\:\frac{\mathrm{y}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}\left(\mathrm{2y}\right)\mathrm{dy} \\ $$$$=\int_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \:\:\:\:\frac{\mathrm{y}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{\mathrm{y}^{\mathrm{2}} −\mathrm{1}}\mathrm{dy}\:=\int_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \:\:\mathrm{dy}\:+\int_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \:\:\:\frac{\mathrm{dy}}{\left(\mathrm{y}−\mathrm{1}\right)\left(\mathrm{y}+\mathrm{1}\right)} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }−\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \:\:\:\left(\frac{\mathrm{1}}{\mathrm{y}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{y}+\mathrm{1}}\right)\mathrm{dy} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }−\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{log}\mid\frac{\mathrm{y}−\mathrm{1}}{\mathrm{y}+\mathrm{1}}\mid\right]_{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }} ^{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }} \\ $$$$=\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }−\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\left\{\mathrm{log}\mid\frac{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} }−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{4}} +\mathrm{1}}}\mid−\mathrm{log}\mid\frac{\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }−\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{e}^{\mathrm{2}} }+\mathrm{1}}\mid\right\} \\ $$
