Question Number 75848 by behi83417@gmail.com last updated on 18/Dec/19
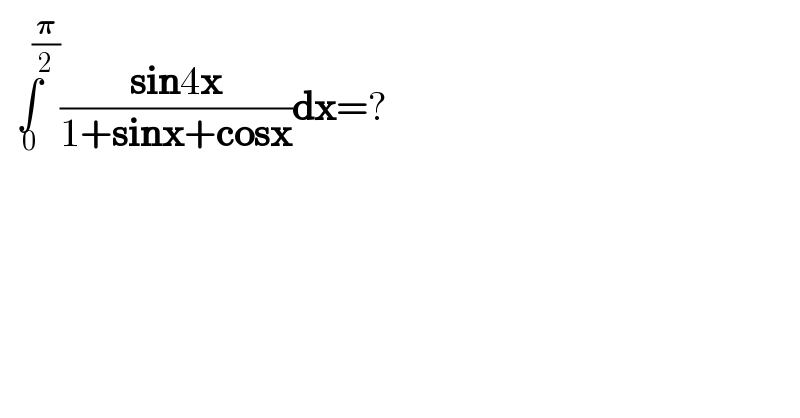
$$\underset{\mathrm{0}} {\overset{\:\:\:\:\:\:\:\:\frac{\boldsymbol{\pi}}{\mathrm{2}}} {\int}}\frac{\boldsymbol{\mathrm{sin}}\mathrm{4}\boldsymbol{\mathrm{x}}}{\mathrm{1}+\boldsymbol{\mathrm{sinx}}+\boldsymbol{\mathrm{cosx}}}\boldsymbol{\mathrm{dx}}=? \\ $$
Commented by mathmax by abdo last updated on 18/Dec/19
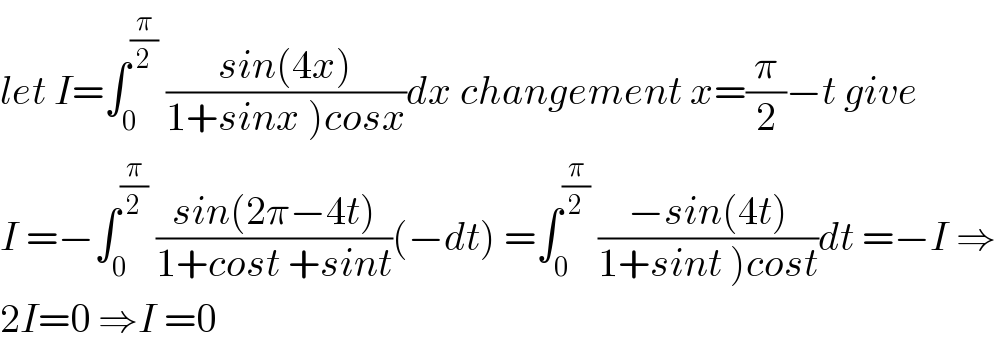
$${let}\:{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{4}{x}\right)}{\left.\mathrm{1}+{sinx}\:\right){cosx}}{dx}\:{changement}\:{x}=\frac{\pi}{\mathrm{2}}−{t}\:{give} \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{sin}\left(\mathrm{2}\pi−\mathrm{4}{t}\right)}{\mathrm{1}+{cost}\:+{sint}}\left(−{dt}\right)\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{−{sin}\left(\mathrm{4}{t}\right)}{\left.\mathrm{1}+{sint}\:\right){cost}}{dt}\:=−{I}\:\Rightarrow \\ $$$$\mathrm{2}{I}=\mathrm{0}\:\Rightarrow{I}\:=\mathrm{0} \\ $$
Answered by MJS last updated on 18/Dec/19
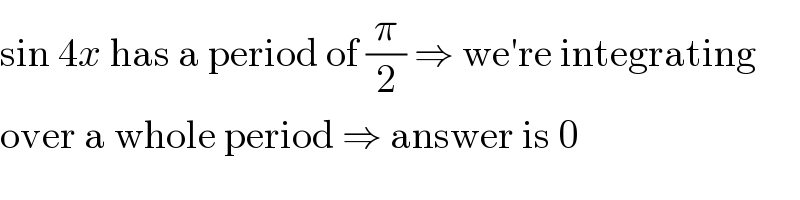
$$\mathrm{sin}\:\mathrm{4}{x}\:\mathrm{has}\:\mathrm{a}\:\mathrm{period}\:\mathrm{of}\:\frac{\pi}{\mathrm{2}}\:\Rightarrow\:\mathrm{we}'\mathrm{re}\:\mathrm{integrating} \\ $$$$\mathrm{over}\:\mathrm{a}\:\mathrm{whole}\:\mathrm{period}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0} \\ $$
Commented by behi83417@gmail.com last updated on 19/Dec/19
$$\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} \boldsymbol{\mathrm{cellent}}\:\boldsymbol{\mathrm{dear}}\:\boldsymbol{\mathrm{proph}}. \\ $$$$\boldsymbol{\mathrm{than}}\mathrm{k}\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{advance}}\:\boldsymbol{\mathrm{sir}}. \\ $$
Answered by MJS last updated on 19/Dec/19
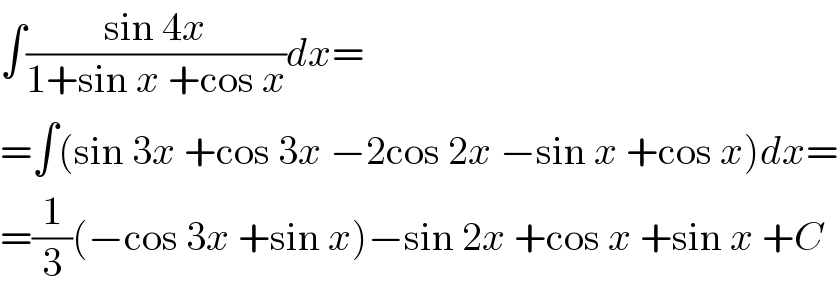
$$\int\frac{\mathrm{sin}\:\mathrm{4}{x}}{\mathrm{1}+\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{dx}= \\ $$$$=\int\left(\mathrm{sin}\:\mathrm{3}{x}\:+\mathrm{cos}\:\mathrm{3}{x}\:−\mathrm{2cos}\:\mathrm{2}{x}\:−\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}\right){dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(−\mathrm{cos}\:\mathrm{3}{x}\:+\mathrm{sin}\:{x}\right)−\mathrm{sin}\:\mathrm{2}{x}\:+\mathrm{cos}\:{x}\:+\mathrm{sin}\:{x}\:+{C} \\ $$
