Question Number 67835 by mind is power last updated on 01/Sep/19
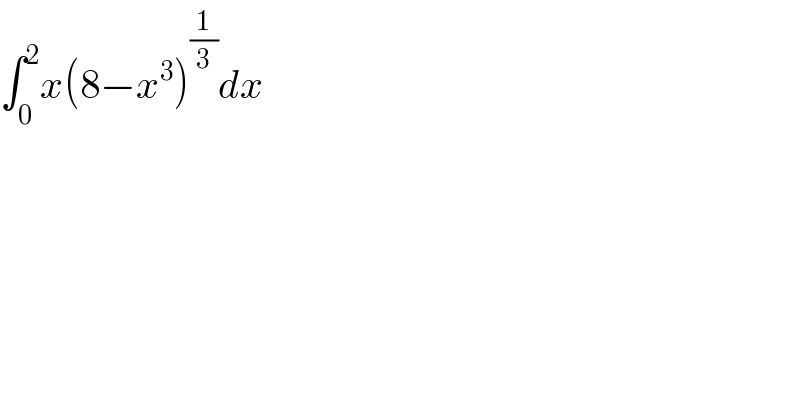
$$\int_{\mathrm{0}} ^{\mathrm{2}} {x}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$
Answered by MJS last updated on 01/Sep/19
![∫x(8−x^3 )^(1/3) = [t=(((8−x^3 )^(1/3) )/x) → dx=−((x^2 (8−x^3 )^(2/3) )/8)dt] =−8∫(t^3 /((t^3 +1)^2 ))dt= now decompose and solve; I get =((8t)/(3(t^3 +1)))+(4/9)ln ((t^2 −t+1)/((t+1)^2 )) −((8(√3))/9)arctan ((2t−1)/( (√3))) = =(1/3)x^2 (8−x^3 )^(1/3) +(4/9)ln ((x^2 −x(8−x^3 )^(1/3) +(8−x^3 )^(2/3) )/((x+(8−x^3 )^(1/3) )^2 )) −((8(√3))/9)arctan ((2(8−x^3 )^(1/3) −x)/( (√3)x)) +Cg ∫_0 ^2 x(8−x^3 )^(1/3) =((16(√3))/(27))π](https://www.tinkutara.com/question/Q67853.png)
$$\int{x}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} = \\ $$$$\:\:\:\:\:\left[{t}=\frac{\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} }{{x}}\:\rightarrow\:{dx}=−\frac{{x}^{\mathrm{2}} \left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{2}/\mathrm{3}} }{\mathrm{8}}{dt}\right] \\ $$$$=−\mathrm{8}\int\frac{{t}^{\mathrm{3}} }{\left({t}^{\mathrm{3}} +\mathrm{1}\right)^{\mathrm{2}} }{dt}= \\ $$$$\:\:\:\:\:\mathrm{now}\:\mathrm{decompose}\:\mathrm{and}\:\mathrm{solve};\:\mathrm{I}\:\mathrm{get} \\ $$$$=\frac{\mathrm{8}{t}}{\mathrm{3}\left({t}^{\mathrm{3}} +\mathrm{1}\right)}+\frac{\mathrm{4}}{\mathrm{9}}\mathrm{ln}\:\frac{{t}^{\mathrm{2}} −{t}+\mathrm{1}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\:= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{2}} \left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} +\frac{\mathrm{4}}{\mathrm{9}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} −{x}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} +\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{2}/\mathrm{3}} }{\left({x}+\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} \right)^{\mathrm{2}} }\:−\frac{\mathrm{8}\sqrt{\mathrm{3}}}{\mathrm{9}}\mathrm{arctan}\:\frac{\mathrm{2}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} −{x}}{\:\sqrt{\mathrm{3}}{x}}\:+{Cg} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}{x}\left(\mathrm{8}−{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} =\frac{\mathrm{16}\sqrt{\mathrm{3}}}{\mathrm{27}}\pi \\ $$
