Menu Close

0-2pi-dx-5-3sin-2x-

Tinku Tara 0 Comments
Pin




Question Number 133305 by liberty last updated on 21/Feb/21
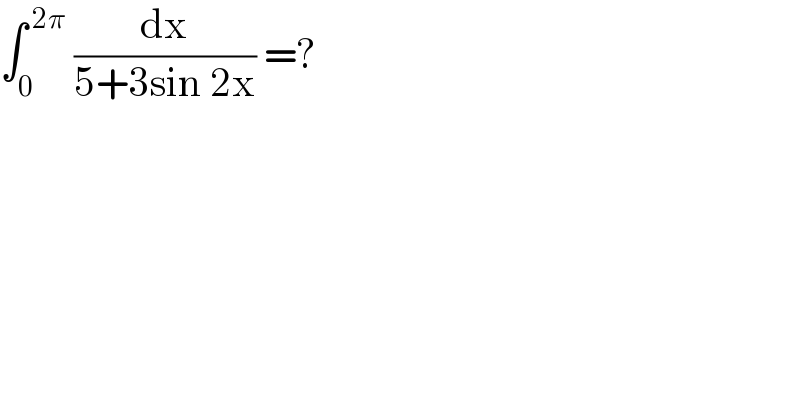
∫_0 ^( 2π) (dx/(5+3sin 2x)) =?
$$\int_{\mathrm{0}} ^{\:\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{5}+\mathrm{3sin}\:\mathrm{2x}}\:=? \\ $$
Answered by physicstutes last updated on 21/Feb/21
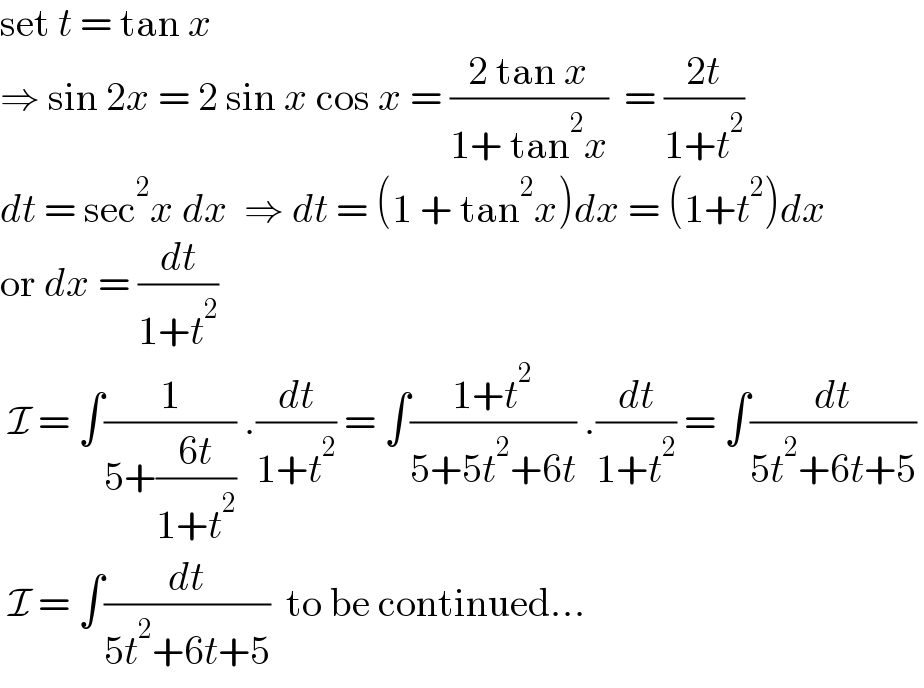
set t = tan x ⇒ sin 2x = 2 sin x cos x = ((2 tan x)/(1+ tan^2 x)) = ((2t)/(1+t^2 )) dt = sec^2 x dx ⇒ dt = (1 + tan^2 x)dx = (1+t^2 )dx or dx = (dt/(1+t^2 )) I = ∫(1/(5+((6t)/(1+t^2 )))) .(dt/(1+t^2 )) = ∫((1+t^2 )/(5+5t^2 +6t)) .(dt/(1+t^2 )) = ∫(dt/(5t^2 +6t+5)) I = ∫(dt/(5t^2 +6t+5)) to be continued...
$$\mathrm{set}\:{t}\:=\:\mathrm{tan}\:{x} \\ $$$$\Rightarrow\:\mathrm{sin}\:\mathrm{2}{x}\:=\:\mathrm{2}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}\:=\:\frac{\mathrm{2}\:\mathrm{tan}\:{x}}{\mathrm{1}+\:\mathrm{tan}^{\mathrm{2}} {x}}\:\:=\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${dt}\:=\:\mathrm{sec}^{\mathrm{2}} {x}\:{dx}\:\:\Rightarrow\:{dt}\:=\:\left(\mathrm{1}\:+\:\mathrm{tan}^{\mathrm{2}} {x}\right){dx}\:=\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right){dx} \\ $$$$\mathrm{or}\:{dx}\:=\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$\:\mathcal{I}\:=\:\int\frac{\mathrm{1}}{\mathrm{5}+\frac{\mathrm{6}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:.\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{5}+\mathrm{5}{t}^{\mathrm{2}} +\mathrm{6}{t}}\:.\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\:\int\frac{{dt}}{\mathrm{5}{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{5}}\: \\ $$$$\:\mathcal{I}\:=\:\int\frac{{dt}}{\mathrm{5}{t}^{\mathrm{2}} +\mathrm{6}{t}+\mathrm{5}}\:\:\mathrm{to}\:\mathrm{be}\:\mathrm{continued}… \\ $$
Commented by Dwaipayan Shikari last updated on 21/Feb/21
(1/5)∫(dt/((t+(3/5))^2 +((4/5))^2 ))=(1/4)tan^(−1) ((t+(3/5))/(4/5))=(1/4)tan^(−1) ((5t+3)/4)+C =(1/4)tan^(−1) ((5tanx+3)/4)+C
$$\frac{\mathrm{1}}{\mathrm{5}}\int\frac{{dt}}{\left({t}+\frac{\mathrm{3}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{5}}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{4}}{tan}^{−\mathrm{1}} \frac{{t}+\frac{\mathrm{3}}{\mathrm{5}}}{\frac{\mathrm{4}}{\mathrm{5}}}=\frac{\mathrm{1}}{\mathrm{4}}{tan}^{−\mathrm{1}} \frac{\mathrm{5}{t}+\mathrm{3}}{\mathrm{4}}+{C} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}{tan}^{−\mathrm{1}} \frac{\mathrm{5}{tanx}+\mathrm{3}}{\mathrm{4}}+{C} \\ $$
Answered by MJS_new last updated on 21/Feb/21
=4∫_(π/4) ^(3π/4) (dx/(5+3sin 2x))= [t=(3/5)+tan x → dx=cos^2 x dt] =−(4/5)∫^(8/5) _(−2/5) (dt/(t^2 +16/25))= =−[arctan ((5t)/4)]_(−2/5) ^(8/5) =(π/2)
$$=\mathrm{4}\underset{\pi/\mathrm{4}} {\overset{\mathrm{3}\pi/\mathrm{4}} {\int}}\frac{{dx}}{\mathrm{5}+\mathrm{3sin}\:\mathrm{2}{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{3}}{\mathrm{5}}+\mathrm{tan}\:{x}\:\rightarrow\:{dx}=\mathrm{cos}^{\mathrm{2}} \:{x}\:{dt}\right] \\ $$$$=−\frac{\mathrm{4}}{\mathrm{5}}\underset{−\mathrm{2}/\mathrm{5}} {\int}^{\mathrm{8}/\mathrm{5}} \frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{16}/\mathrm{25}}= \\ $$$$=−\left[\mathrm{arctan}\:\frac{\mathrm{5}{t}}{\mathrm{4}}\right]_{−\mathrm{2}/\mathrm{5}} ^{\mathrm{8}/\mathrm{5}} =\frac{\pi}{\mathrm{2}} \\ $$
Commented by liberty last updated on 22/Feb/21
yes....correct
$$\mathrm{yes}….\mathrm{correct} \\ $$
Answered by mathmax by abdo last updated on 21/Feb/21
I =∫_0 ^(2π) (dx/(5+3sin(2x))) ⇒I =_(2x=t) ∫_0 ^(4π) (dt/(2(5+3sint))) ⇒2I =∫_0 ^(2π) (dt/(5+3sint)) +∫_(2π) ^(4π) (dt/(5+3sint))(t=2π+u) =∫_0 ^(2π) (dt/(5+3sint))+∫_0 ^(2π) (du/(5+3sinu)) =2∫_0 ^(2π) (dt/(5+3sint)) ⇒ I =∫_0 ^(2π) (dt/(5+3sint)) =_(z=e^(it) ) ∫_(∣z∣=1) (dz/(iz(5+3((z−z^(−1) )/(2i))))) =∫_(∣z∣=1) ((2idz)/(iz(10i+3z−3z^(−1) ))) =∫_(∣z∣=1) ((2dz)/(10iz+3z^2 −3)) =∫_(∣z∣=1) ((2dz)/(3z^2 +10iz−3)) ϕ(z)=(2/(3z^2 +10iz−3)) Δ^′ =(5i)^2 +9 =9−25 =−16 ⇒z_1 =((−5i+4i)/3)=−(1/3)i z_2 =((−5i−4i)/3) =−3i ⇒∣z_2 ∣>1 (out ) ⇒ϕ(z)=(2/(3(z−z_1 )(z−z_2 ))) ∫_(∣z∣=1) ϕ(z)dz =2iπRes(ϕ,z_1 ) =2iπ×(2/(3(z_1 −z_2 ))) =((4iπ)/(3.(−(1/3)i−3i))) =((4iπ)/(−i−9i)) =((4iπ)/(−10i)) =−((4π)/(10)) =−((2π)/5) ⇒ I =−((2π)/5)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dx}}{\mathrm{5}+\mathrm{3sin}\left(\mathrm{2x}\right)}\:\Rightarrow\mathrm{I}\:=_{\mathrm{2x}=\mathrm{t}} \:\:\:\int_{\mathrm{0}} ^{\mathrm{4}\pi} \:\frac{\mathrm{dt}}{\mathrm{2}\left(\mathrm{5}+\mathrm{3sint}\right)} \\ $$$$\Rightarrow\mathrm{2I}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3sint}}\:+\int_{\mathrm{2}\pi} ^{\mathrm{4}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3sint}}\left(\mathrm{t}=\mathrm{2}\pi+\mathrm{u}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3sint}}+\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{du}}{\mathrm{5}+\mathrm{3sinu}}\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3sint}}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\frac{\mathrm{dt}}{\mathrm{5}+\mathrm{3sint}}\:=_{\mathrm{z}=\mathrm{e}^{\mathrm{it}} } \:\:\:\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\frac{\mathrm{dz}}{\mathrm{iz}\left(\mathrm{5}+\mathrm{3}\frac{\mathrm{z}−\mathrm{z}^{−\mathrm{1}} }{\mathrm{2i}}\right)} \\ $$$$=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2idz}}{\mathrm{iz}\left(\mathrm{10i}+\mathrm{3z}−\mathrm{3z}^{−\mathrm{1}} \right)}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\frac{\mathrm{2dz}}{\mathrm{10iz}+\mathrm{3z}^{\mathrm{2}} −\mathrm{3}}\:=\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\frac{\mathrm{2dz}}{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{10iz}−\mathrm{3}} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{2}}{\mathrm{3z}^{\mathrm{2}} \:+\mathrm{10iz}−\mathrm{3}} \\ $$$$\Delta^{'} \:=\left(\mathrm{5i}\right)^{\mathrm{2}} +\mathrm{9}\:=\mathrm{9}−\mathrm{25}\:=−\mathrm{16}\:\Rightarrow\mathrm{z}_{\mathrm{1}} =\frac{−\mathrm{5i}+\mathrm{4i}}{\mathrm{3}}=−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{i} \\ $$$$\mathrm{z}_{\mathrm{2}} =\frac{−\mathrm{5i}−\mathrm{4i}}{\mathrm{3}}\:=−\mathrm{3i}\:\Rightarrow\mid\mathrm{z}_{\mathrm{2}} \mid>\mathrm{1}\:\left(\mathrm{out}\:\right)\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{z}−\mathrm{z}_{\mathrm{1}} \right)\left(\mathrm{z}−\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$\int_{\mid\mathrm{z}\mid=\mathrm{1}} \:\:\:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\mathrm{Res}\left(\varphi,\mathrm{z}_{\mathrm{1}} \right)\:=\mathrm{2i}\pi×\frac{\mathrm{2}}{\mathrm{3}\left(\mathrm{z}_{\mathrm{1}} −\mathrm{z}_{\mathrm{2}} \right)} \\ $$$$=\frac{\mathrm{4i}\pi}{\mathrm{3}.\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{i}−\mathrm{3i}\right)}\:=\frac{\mathrm{4i}\pi}{−\mathrm{i}−\mathrm{9i}}\:=\frac{\mathrm{4i}\pi}{−\mathrm{10i}}\:=−\frac{\mathrm{4}\pi}{\mathrm{10}}\:=−\frac{\mathrm{2}\pi}{\mathrm{5}}\:\Rightarrow \\ $$$$\mathrm{I}\:=−\frac{\mathrm{2}\pi}{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *