Question Number 544 by 123456 last updated on 26/Jan/15
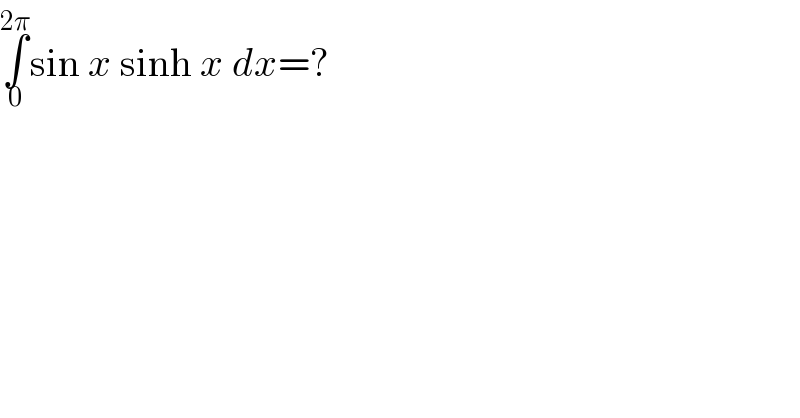
$$\underset{\mathrm{0}} {\overset{\mathrm{2}\pi} {\int}}\mathrm{sin}\:{x}\:\mathrm{sinh}\:{x}\:{dx}=? \\ $$
Answered by prakash jain last updated on 26/Jan/15
![∫sin x sinh xdx =sin x cosh x −∫cos x cosh x dx =sin x cosh x − [cos x sinh x +∫sin x sinh x dx] =(1/2)(sin x cosh x−cos x sinh x) putting the limits (1/2)(−sinh 2π) =− ((sinh 2π)/2)= − sinh π cosh π](https://www.tinkutara.com/question/Q555.png)
$$\int\mathrm{sin}\:{x}\:\mathrm{sinh}\:{xdx} \\ $$$$=\mathrm{sin}\:{x}\:\mathrm{cosh}\:{x}\:−\int\mathrm{cos}\:{x}\:\mathrm{cosh}\:{x}\:{dx} \\ $$$$=\mathrm{sin}\:{x}\:\mathrm{cosh}\:{x}\:−\:\left[\mathrm{cos}\:{x}\:\mathrm{sinh}\:{x}\:+\int\mathrm{sin}\:{x}\:\mathrm{sinh}\:{x}\:{dx}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{sin}\:{x}\:\mathrm{cosh}\:{x}−\mathrm{cos}\:{x}\:\mathrm{sinh}\:{x}\right) \\ $$$${putting}\:{the}\:{limits} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(−\mathrm{sinh}\:\mathrm{2}\pi\right) \\ $$$$=−\:\frac{\mathrm{sinh}\:\mathrm{2}\pi}{\mathrm{2}}=\:−\:\mathrm{sinh}\:\pi\:\mathrm{cosh}\:\pi \\ $$
