Question Number 77675 by TawaTawa last updated on 08/Jan/20
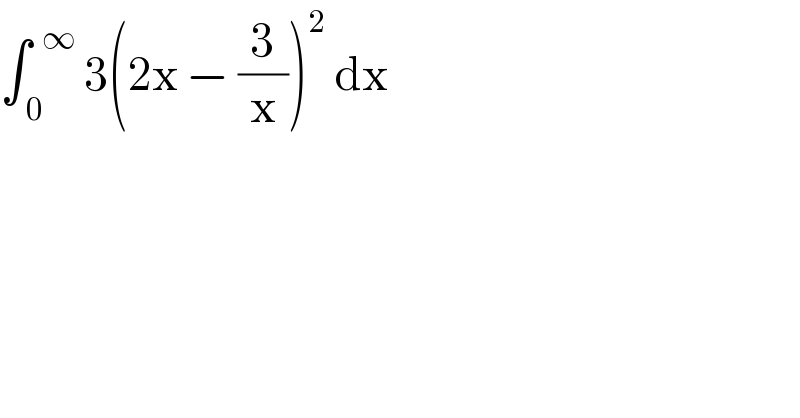
$$\int_{\:\mathrm{0}} ^{\:\:\infty} \:\mathrm{3}\left(\mathrm{2x}\:−\:\frac{\mathrm{3}}{\mathrm{x}}\right)^{\mathrm{2}} \:\mathrm{dx} \\ $$
Answered by mind is power last updated on 09/Jan/20
![diverge use that[(2x−(3/x))]^2 ≥1,∀x≥4 ⇒∫_0 ^(+∞) 3(2x−(3/x))^2 dx≥∫_4 ^(+∞) 3.4dx=∫_3 ^(+∞) 12dx=+∞](https://www.tinkutara.com/question/Q77684.png)
$$\mathrm{diverge}\: \\ $$$$\mathrm{use}\:\mathrm{that}\left[\left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{x}}\right)\right]^{\mathrm{2}} \geqslant\mathrm{1},\forall\mathrm{x}\geqslant\mathrm{4}\: \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \mathrm{3}\left(\mathrm{2x}−\frac{\mathrm{3}}{\mathrm{x}}\right)^{\mathrm{2}} \mathrm{dx}\geqslant\int_{\mathrm{4}} ^{+\infty} \mathrm{3}.\mathrm{4dx}=\int_{\mathrm{3}} ^{+\infty} \mathrm{12dx}=+\infty \\ $$
Commented by TawaTawa last updated on 09/Jan/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
