Question Number 137448 by liberty last updated on 03/Apr/21
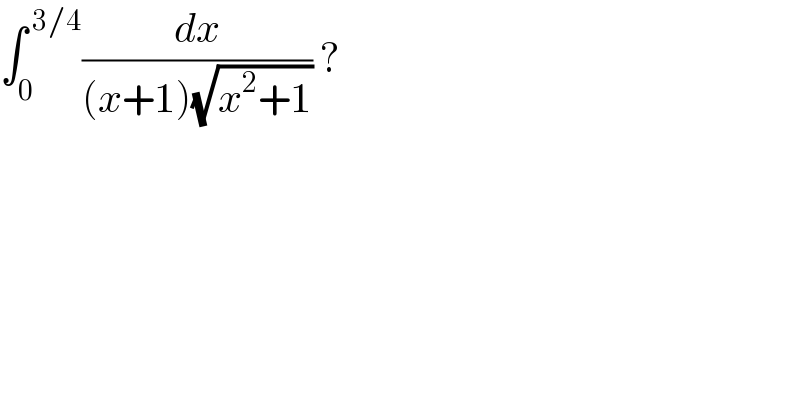
$$\int_{\mathrm{0}} ^{\:\mathrm{3}/\mathrm{4}} \frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}\:? \\ $$
Answered by MJS_new last updated on 03/Apr/21
![∫(dx/((x+1)(√(x^2 +1))))= [t=x+(√(x^2 +1)) ⇔ x=((t^2 −1)/(2t)) → dx=((√(x^2 +1))/(x+(√(x^2 +1))))dt] =2∫(dt/(t^2 +2t−1))=−((√2)/2)ln ((t+1+(√2))/(t+1−(√2))) = =−((√2)/2)ln ((−x+1+(√(2(x^2 +1))))/(x+1)) ⇒ answer is (ln (1+2(√2)) −(1/2)ln 7)(√2)](https://www.tinkutara.com/question/Q137453.png)
$$\int\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}={x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\:\Leftrightarrow\:{x}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{t}}\:\rightarrow\:{dx}=\frac{\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{{x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\frac{{t}+\mathrm{1}+\sqrt{\mathrm{2}}}{{t}+\mathrm{1}−\sqrt{\mathrm{2}}}\:= \\ $$$$=−\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\frac{−{x}+\mathrm{1}+\sqrt{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}}{{x}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\left(\mathrm{ln}\:\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\mathrm{7}\right)\sqrt{\mathrm{2}} \\ $$
Commented by liberty last updated on 03/Apr/21
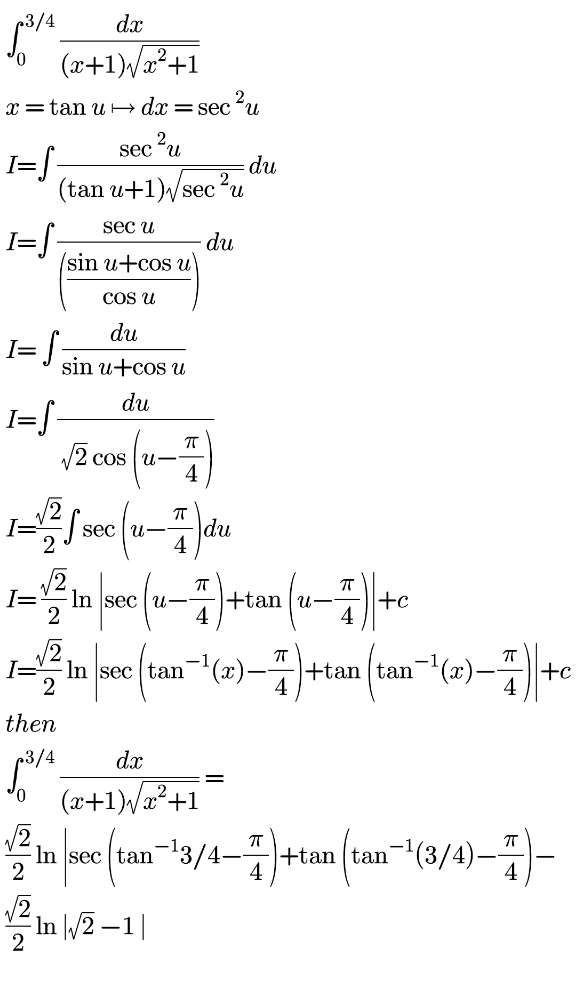
Commented by liberty last updated on 03/Apr/21
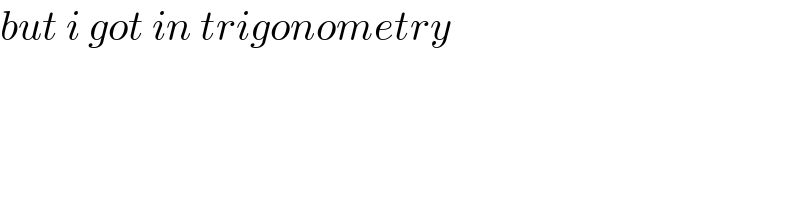
$${but}\:{i}\:{got}\:{in}\:{trigonometry} \\ $$
Answered by EDWIN88 last updated on 03/Apr/21
![E= ∫_0 ^( 3/4) (dx/((x+1)(√(x^2 +1)))) let x = tan t ⇒dx = sec^2 t dt E=∫^ ((sec^2 t )/((tan t +1)(√(1+tan^2 t)))) dt E= ∫ (dt/( (√2) sec (t−(π/4)))) = (1/( (√2))) ln ∣sec (t−(π/4))+tan (t−(π/4))∣+C = (1/( (√2))) ln ∣ (((√2) sec t+tan t−1)/(1+tan t))∣ + C =(1/( (√2))) ln ∣(((√(2+2x^2 )) +x−1)/(1+x)) ∣ + C Now ∫_0 ^( 3/4) (dx/((x+1)(√(1+x^2 )))) = (1/( (√2))) [ ln (2(√(14)) −1)−ln (7)−ln ((√2) −1) ] ≈ 0.569006](https://www.tinkutara.com/question/Q137498.png)
$$\mathrm{E}=\:\int_{\mathrm{0}} ^{\:\mathrm{3}/\mathrm{4}} \:\frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{let}\:\mathrm{x}\:=\:\mathrm{tan}\:\mathrm{t}\:\Rightarrow\mathrm{dx}\:=\:\mathrm{sec}^{\mathrm{2}} \:\mathrm{t}\:\mathrm{dt}\: \\ $$$$\mathrm{E}=\int^{\:} \:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{t}\:}{\left(\mathrm{tan}\:\mathrm{t}\:+\mathrm{1}\right)\sqrt{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \mathrm{t}}}\:\mathrm{dt} \\ $$$$\mathrm{E}=\:\int\:\frac{\mathrm{dt}}{\:\sqrt{\mathrm{2}}\:\mathrm{sec}\:\left(\mathrm{t}−\frac{\pi}{\mathrm{4}}\right)}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\mid\mathrm{sec}\:\left(\mathrm{t}−\frac{\pi}{\mathrm{4}}\right)+\mathrm{tan}\:\left(\mathrm{t}−\frac{\pi}{\mathrm{4}}\right)\mid+\mathrm{C} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\mid\:\frac{\sqrt{\mathrm{2}}\:\mathrm{sec}\:\mathrm{t}+\mathrm{tan}\:\mathrm{t}−\mathrm{1}}{\mathrm{1}+\mathrm{tan}\:\mathrm{t}}\mid\:+\:\mathrm{C} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{2}+\mathrm{2x}^{\mathrm{2}} }\:+\mathrm{x}−\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:\mid\:+\:\mathrm{C} \\ $$$$\mathrm{Now}\:\int_{\mathrm{0}} ^{\:\mathrm{3}/\mathrm{4}} \:\frac{{dx}}{\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\: \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\left[\:\mathrm{ln}\:\left(\mathrm{2}\sqrt{\mathrm{14}}\:−\mathrm{1}\right)−\mathrm{ln}\:\left(\mathrm{7}\right)−\mathrm{ln}\:\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)\:\right] \\ $$$$\approx\:\mathrm{0}.\mathrm{569006} \\ $$
