Question Number 136905 by leena12345 last updated on 27/Mar/21
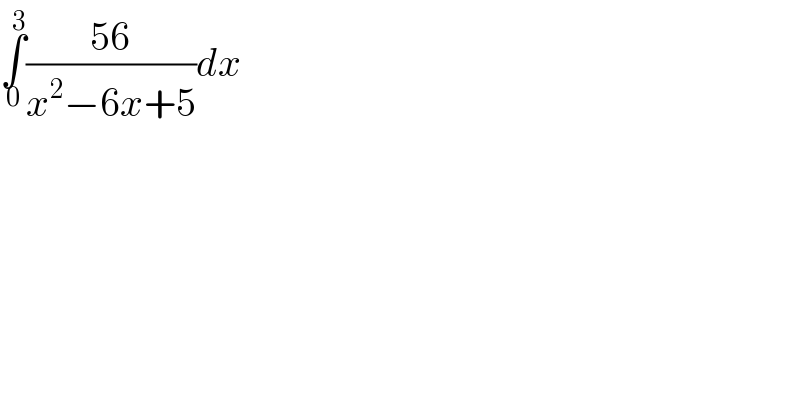
$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\frac{\mathrm{56}}{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}}{dx} \\ $$
Answered by Mathspace last updated on 27/Mar/21
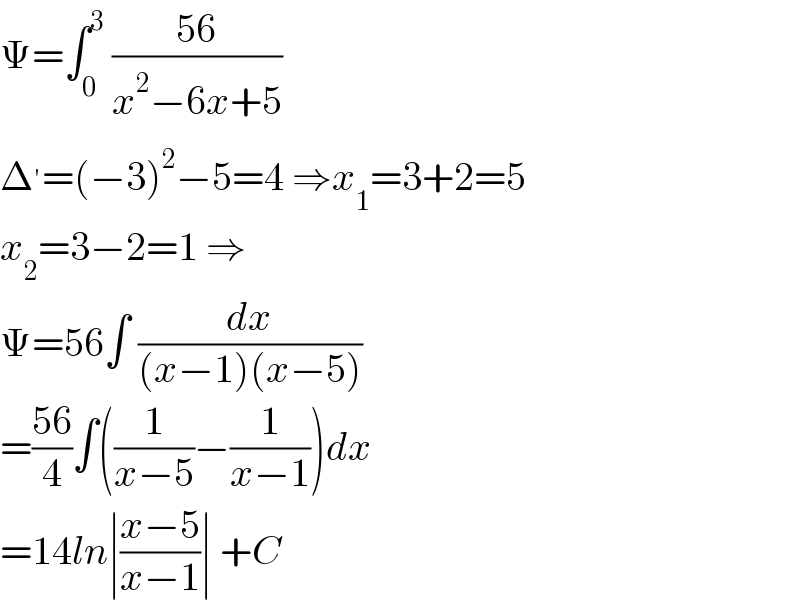
$$\Psi=\int_{\mathrm{0}} ^{\mathrm{3}} \:\frac{\mathrm{56}}{{x}^{\mathrm{2}} −\mathrm{6}{x}+\mathrm{5}} \\ $$$$\Delta^{'} =\left(−\mathrm{3}\right)^{\mathrm{2}} −\mathrm{5}=\mathrm{4}\:\Rightarrow{x}_{\mathrm{1}} =\mathrm{3}+\mathrm{2}=\mathrm{5} \\ $$$${x}_{\mathrm{2}} =\mathrm{3}−\mathrm{2}=\mathrm{1}\:\Rightarrow \\ $$$$\Psi=\mathrm{56}\int\:\frac{{dx}}{\left({x}−\mathrm{1}\right)\left({x}−\mathrm{5}\right)} \\ $$$$=\frac{\mathrm{56}}{\mathrm{4}}\int\left(\frac{\mathrm{1}}{{x}−\mathrm{5}}−\frac{\mathrm{1}}{{x}−\mathrm{1}}\right){dx} \\ $$$$=\mathrm{14}{ln}\mid\frac{{x}−\mathrm{5}}{{x}−\mathrm{1}}\mid\:+{C} \\ $$
Commented by Mathspace last updated on 27/Mar/21
![Ψ=14[ln∣((x−5)/(x−1))∣]_0 ^3 =14{ln(1)−ln(5)}=−14ln(5)](https://www.tinkutara.com/question/Q136917.png)
$$\Psi=\mathrm{14}\left[{ln}\mid\frac{{x}−\mathrm{5}}{{x}−\mathrm{1}}\mid\right]_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$=\mathrm{14}\left\{{ln}\left(\mathrm{1}\right)−{ln}\left(\mathrm{5}\right)\right\}=−\mathrm{14}{ln}\left(\mathrm{5}\right) \\ $$
