Question Number 76724 by Rio Michael last updated on 29/Dec/19
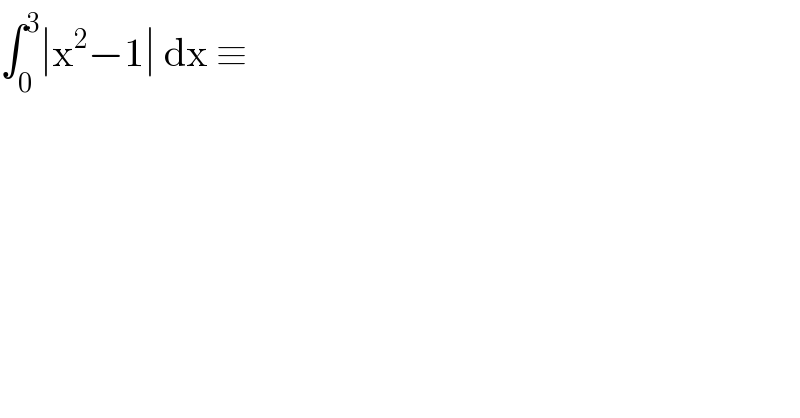
$$\int_{\mathrm{0}} ^{\mathrm{3}} \mid\mathrm{x}^{\mathrm{2}} −\mathrm{1}\mid\:\mathrm{dx}\:\equiv\: \\ $$
Commented by abdomathmax last updated on 30/Dec/19
![∫_0 ^3 ∣x^2 −1∣dx =∫_0 ^1 (1−x^2 )dx +∫_1 ^3 (x^2 −1)dx =[x−(x^3 /3)]_0 ^1 +[(x^3 /3)−x]_1 ^3 =1−(1/3) +(3^2 −3)−((1/3)−1) =(2/3) +6+(2/3) =(4/3)+6 =((22)/3)](https://www.tinkutara.com/question/Q76748.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \mid{x}^{\mathrm{2}} −\mathrm{1}\mid{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}\:+\int_{\mathrm{1}} ^{\mathrm{3}} \left({x}^{\mathrm{2}} −\mathrm{1}\right){dx} \\ $$$$=\left[{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}\right]_{\mathrm{1}} ^{\mathrm{3}} =\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\:+\left(\mathrm{3}^{\mathrm{2}} −\mathrm{3}\right)−\left(\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\:+\mathrm{6}+\frac{\mathrm{2}}{\mathrm{3}}\:=\frac{\mathrm{4}}{\mathrm{3}}+\mathrm{6}\:=\frac{\mathrm{22}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by MJS last updated on 30/Dec/19
![x^2 −1=0 ⇒ x=±1 0≤x<1: x^2 −1<0 ⇒ ∣x^2 −1∣=1−x^2 1≤x≤3: x^2 −1≥0 ⇒ ∣x^2 −1∣=x^2 −1 ∫_0 ^3 ∣x^2 −1∣dx=∫_0 ^1 (1−x^2 )dx+∫_1 ^3 (x^2 −1)dx= =[x−(x^3 /3)]_0 ^1 +[(x^3 /3)−x]_1 ^3 =((2/3)−0)+(6+(2/3))=((22)/3)](https://www.tinkutara.com/question/Q76730.png)
$${x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow\:{x}=\pm\mathrm{1} \\ $$$$\mathrm{0}\leqslant{x}<\mathrm{1}:\:{x}^{\mathrm{2}} −\mathrm{1}<\mathrm{0}\:\Rightarrow\:\mid{x}^{\mathrm{2}} −\mathrm{1}\mid=\mathrm{1}−{x}^{\mathrm{2}} \\ $$$$\mathrm{1}\leqslant{x}\leqslant\mathrm{3}:\:{x}^{\mathrm{2}} −\mathrm{1}\geqslant\mathrm{0}\:\Rightarrow\:\mid{x}^{\mathrm{2}} −\mathrm{1}\mid={x}^{\mathrm{2}} −\mathrm{1} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mid{x}^{\mathrm{2}} −\mathrm{1}\mid{dx}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{1}−{x}^{\mathrm{2}} \right){dx}+\underset{\mathrm{1}} {\overset{\mathrm{3}} {\int}}\left({x}^{\mathrm{2}} −\mathrm{1}\right){dx}= \\ $$$$=\left[{x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}\right]_{\mathrm{1}} ^{\mathrm{3}} =\left(\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{0}\right)+\left(\mathrm{6}+\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\mathrm{22}}{\mathrm{3}} \\ $$
Commented by Rio Michael last updated on 30/Dec/19

$$\mathrm{thanks} \\ $$
