Question Number 135145 by ZiYangLee last updated on 10/Mar/21
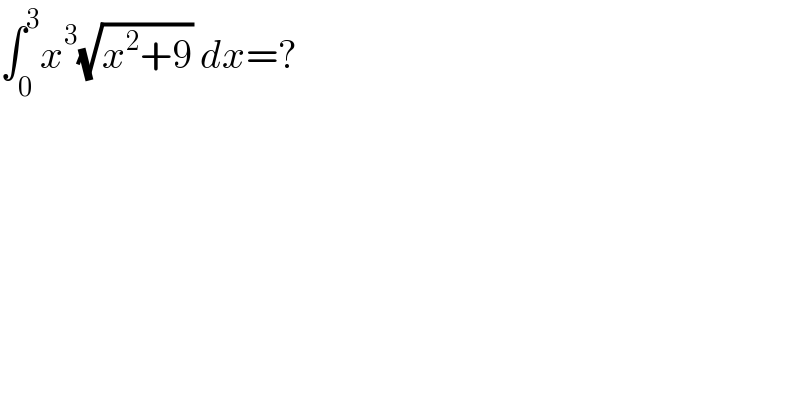
$$\int_{\mathrm{0}} ^{\mathrm{3}} {x}^{\mathrm{3}} \sqrt{{x}^{\mathrm{2}} +\mathrm{9}}\:{dx}=? \\ $$
Answered by bramlexs22 last updated on 10/Mar/21
![∫_0 ^( 3) x^2 .x(√(x^2 +9)) dx = X let x^2 +9 = φ^2 ⇒xdx = φdφ X=∫_3 ^( 3(√2)) (φ^2 −9)φ .(φdφ) = ∫_0 ^( 3(√2) ) (φ^4 −9φ)dφ = [(1/5)φ^5 −3φ^2 ]_3 ^(3(√2)) = (1/5)(243×4(√2)−243)−3(9) =((243(4(√2)−1))/5)−27](https://www.tinkutara.com/question/Q135163.png)
$$\int_{\mathrm{0}} ^{\:\mathrm{3}} \:\mathrm{x}^{\mathrm{2}} .\mathrm{x}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{9}}\:\mathrm{dx}\:=\:\mathcal{X} \\ $$$$\mathrm{let}\:\mathrm{x}^{\mathrm{2}} +\mathrm{9}\:=\:\phi^{\mathrm{2}} \:\Rightarrow\mathrm{xdx}\:=\:\phi\mathrm{d}\phi\: \\ $$$$\mathcal{X}=\int_{\mathrm{3}} ^{\:\mathrm{3}\sqrt{\mathrm{2}}} \left(\phi^{\mathrm{2}} −\mathrm{9}\right)\phi\:.\left(\phi\mathrm{d}\phi\right) \\ $$$$=\:\int_{\mathrm{0}} ^{\:\mathrm{3}\sqrt{\mathrm{2}}\:} \left(\phi^{\mathrm{4}} −\mathrm{9}\phi\right)\mathrm{d}\phi \\ $$$$=\:\left[\frac{\mathrm{1}}{\mathrm{5}}\phi^{\mathrm{5}} −\mathrm{3}\phi^{\mathrm{2}} \:\right]_{\mathrm{3}} ^{\mathrm{3}\sqrt{\mathrm{2}}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{5}}\left(\mathrm{243}×\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{243}\right)−\mathrm{3}\left(\mathrm{9}\right) \\ $$$$=\frac{\mathrm{243}\left(\mathrm{4}\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\mathrm{5}}−\mathrm{27} \\ $$
