Question Number 139889 by qaz last updated on 02/May/21
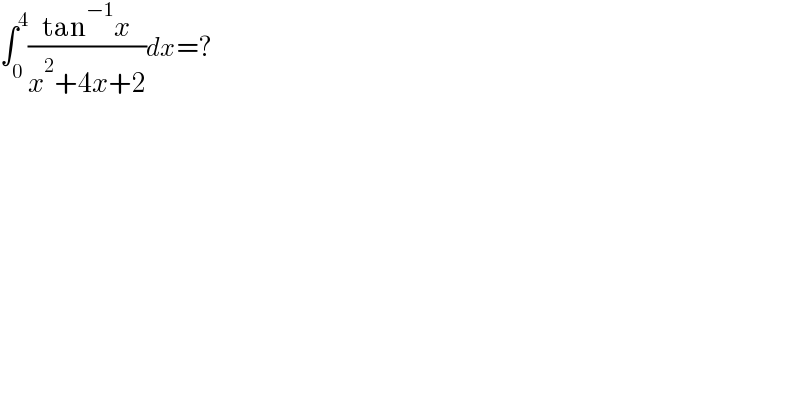
$$\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{dx}=? \\ $$
Commented by qaz last updated on 02/May/21

$${I}=\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{dx} \\ $$$${x}=\frac{\mathrm{4}+{u}}{\mathrm{1}−\mathrm{4}{u}}\:\:\:\:\:\:\left\{{or}\:\:{x}=\frac{\mathrm{4}−{u}}{\mathrm{1}+\mathrm{4}{u}}\right\} \\ $$$$\Rightarrow{dx}=\frac{\mathrm{4}+{u}}{\mathrm{1}−\mathrm{4}{u}}\left(\frac{\mathrm{1}}{\mathrm{4}+{u}}+\frac{\mathrm{4}}{\mathrm{1}−\mathrm{4}{u}}\right){du}=\frac{\mathrm{17}}{\left(\mathrm{1}−\mathrm{4}{u}\right)^{\mathrm{2}} }{du} \\ $$$${I}=\int_{−\mathrm{4}} ^{\mathrm{0}} \frac{\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}+{u}}{\mathrm{1}−\mathrm{4}{u}}}{\left(\frac{\mathrm{4}+{u}}{\mathrm{1}−\mathrm{4}{u}}\right)^{\mathrm{2}} +\mathrm{4}\centerdot\frac{\mathrm{4}+{u}}{\mathrm{1}−\mathrm{4}{u}}+\mathrm{2}}\centerdot\frac{\mathrm{17}}{\left(\mathrm{1}−\mathrm{4}{u}\right)^{\mathrm{2}} }{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}−{u}}{\mathrm{1}+\mathrm{4}{u}}}{{u}^{\mathrm{2}} +\mathrm{4}{u}+\mathrm{2}}{du} \\ $$$$\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{tan}^{−\mathrm{1}} {x}+\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{4}−{x}}{\mathrm{1}+\mathrm{4}{x}}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{4}{x}+\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{tan}^{−\mathrm{1}} \mathrm{4}}{\:\mathrm{4}\sqrt{\mathrm{2}}}{ln}\frac{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Answered by mathmax by abdo last updated on 02/May/21
![I =∫_0 ^4 ((arctanx)/(x^2 +4x+2))dx let f(a) =∫_0 ^4 ((arctan(ax))/(x^2 +4x+2))dx ⇒ f^′ (a) =∫_0 ^4 (x/((1+a^2 x^2 )(x^2 +4x+2)))dx =_(ax=t) ∫_0 ^(4a) (t/(a(1+t^2 )((t^2 /a^2 )+((4t)/a)+2)))(dt/a) =∫_0 ^(4a) ((tdt)/((1+t^2 )(t^2 +4at +2a^2 ))) let decompose F(t)=(t/((t^2 +1)(t^2 +4at +2a^2 ))) t^2 +4at +2a^2 =0→Δ^′ =4a^2 −2a^2 =2a^2 ⇒ t_1 =−2a+(√2)a ant t_2 =−2a−(√2)a ⇒F(t)=(t/((t−t_1 )(t−t_2 )(t^2 +1))) =(α/(t−t_1 ))+(b/(t−t_2 )) +((ct +d)/(t^2 +1)) α=(t_1 /(2(√2)a(t_1 ^2 +1))) and b=(t_2 /(−2(√2)a(t_2 ^2 +1))) c=.... and d=... ⇒∫_0 ^(4a) F(t)dt =α[ln∣t−t_1 ∣]_0 ^(4a) +b[ln∣t−t_2 ∣]_0 ^(4a) +(c/2)[ln(t^2 +1)]_0 ^(4a) +d [arctant]_0 ^(4a) =α{ln∣4a−t_1 ∣−ln∣t_1 ∣}+b{ln∣4a−t_2 ∣−ln∣t_2 ∣} +(c/2)ln(16a^2 +1) +d arctan(4a) =f^′ (a) ⇒ f(a) =∫ ln∣((4a−t_1 )/(t_1 ))∣α(a)da +b∫ ln∣((4a−t_2 )/t_2 )∣b(α)da +(1/2)∫ ln(16a^2 +1)c(a)da +∫ arctan(4a)d(a)da ....be continued....](https://www.tinkutara.com/question/Q139958.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{arctanx}}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{2}}\mathrm{dx}\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{arctan}\left(\mathrm{ax}\right)}{\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{2}}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{4}} \:\frac{\mathrm{x}}{\left(\mathrm{1}+\mathrm{a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{4x}+\mathrm{2}\right)}\mathrm{dx}\:=_{\mathrm{ax}=\mathrm{t}} \:\:\int_{\mathrm{0}} ^{\mathrm{4a}} \:\frac{\mathrm{t}}{\mathrm{a}\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{a}^{\mathrm{2}} }+\frac{\mathrm{4t}}{\mathrm{a}}+\mathrm{2}\right)}\frac{\mathrm{dt}}{\mathrm{a}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{4a}} \:\frac{\mathrm{tdt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4at}\:+\mathrm{2a}^{\mathrm{2}} \right)}\:\mathrm{let}\:\mathrm{decompose}\: \\ $$$$\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{4at}\:+\mathrm{2a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{t}^{\mathrm{2}} \:+\mathrm{4at}\:+\mathrm{2a}^{\mathrm{2}} =\mathrm{0}\rightarrow\Delta^{'} \:=\mathrm{4a}^{\mathrm{2}} −\mathrm{2a}^{\mathrm{2}} \:=\mathrm{2a}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{t}_{\mathrm{1}} =−\mathrm{2a}+\sqrt{\mathrm{2}}\mathrm{a}\:\:\mathrm{ant}\:\mathrm{t}_{\mathrm{2}} =−\mathrm{2a}−\sqrt{\mathrm{2}}\mathrm{a}\:\Rightarrow\mathrm{F}\left(\mathrm{t}\right)=\frac{\mathrm{t}}{\left(\mathrm{t}−\mathrm{t}_{\mathrm{1}} \right)\left(\mathrm{t}−\mathrm{t}_{\mathrm{2}} \right)\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)} \\ $$$$=\frac{\alpha}{\mathrm{t}−\mathrm{t}_{\mathrm{1}} }+\frac{\mathrm{b}}{\mathrm{t}−\mathrm{t}_{\mathrm{2}} }\:+\frac{\mathrm{ct}\:+\mathrm{d}}{\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\alpha=\frac{\mathrm{t}_{\mathrm{1}} }{\mathrm{2}\sqrt{\mathrm{2}}\mathrm{a}\left(\mathrm{t}_{\mathrm{1}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:\mathrm{and}\:\mathrm{b}=\frac{\mathrm{t}_{\mathrm{2}} }{−\mathrm{2}\sqrt{\mathrm{2}}\mathrm{a}\left(\mathrm{t}_{\mathrm{2}} ^{\mathrm{2}} \:+\mathrm{1}\right)}\:\:\mathrm{c}=….\:\mathrm{and}\:\mathrm{d}=… \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{4a}} \:\mathrm{F}\left(\mathrm{t}\right)\mathrm{dt}\:=\alpha\left[\mathrm{ln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{1}} \mid\right]_{\mathrm{0}} ^{\mathrm{4a}} +\mathrm{b}\left[\mathrm{ln}\mid\mathrm{t}−\mathrm{t}_{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\mathrm{4a}} +\frac{\mathrm{c}}{\mathrm{2}}\left[\mathrm{ln}\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{4a}} \\ $$$$+\mathrm{d}\:\left[\mathrm{arctant}\right]_{\mathrm{0}} ^{\mathrm{4a}} \\ $$$$=\alpha\left\{\mathrm{ln}\mid\mathrm{4a}−\mathrm{t}_{\mathrm{1}} \mid−\mathrm{ln}\mid\mathrm{t}_{\mathrm{1}} \mid\right\}+\mathrm{b}\left\{\mathrm{ln}\mid\mathrm{4a}−\mathrm{t}_{\mathrm{2}} \mid−\mathrm{ln}\mid\mathrm{t}_{\mathrm{2}} \mid\right\} \\ $$$$+\frac{\mathrm{c}}{\mathrm{2}}\mathrm{ln}\left(\mathrm{16a}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\mathrm{d}\:\mathrm{arctan}\left(\mathrm{4a}\right)\:=\mathrm{f}^{'} \left(\mathrm{a}\right)\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)\:=\int\:\:\mathrm{ln}\mid\frac{\mathrm{4a}−\mathrm{t}_{\mathrm{1}} }{\mathrm{t}_{\mathrm{1}} \:}\mid\alpha\left(\mathrm{a}\right)\mathrm{da}\:+\mathrm{b}\int\:\mathrm{ln}\mid\frac{\mathrm{4a}−\mathrm{t}_{\mathrm{2}} }{\mathrm{t}_{\mathrm{2}} }\mid\mathrm{b}\left(\alpha\right)\mathrm{da} \\ $$$$+\frac{\mathrm{1}}{\mathrm{2}}\int\:\mathrm{ln}\left(\mathrm{16a}^{\mathrm{2}} \:+\mathrm{1}\right)\mathrm{c}\left(\mathrm{a}\right)\mathrm{da}\:+\int\:\mathrm{arctan}\left(\mathrm{4a}\right)\mathrm{d}\left(\mathrm{a}\right)\mathrm{da} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$
Commented by qaz last updated on 03/May/21
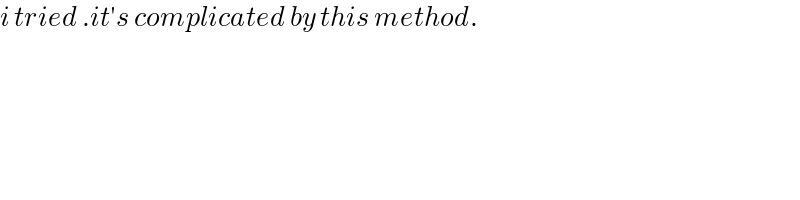
$${i}\:{tried}\:.{it}'{s}\:{complicated}\:{by}\:{this}\:{method}. \\ $$
