Menu Close

0-5-log-10-x-2-55x-90-log-10-x-36-log-10-2-Find-the-value-s-of-x-and-determine-the-domain-of-x-

Tinku Tara 0 Comments
Pin




Question Number 4457 by love math last updated on 29/Jan/16
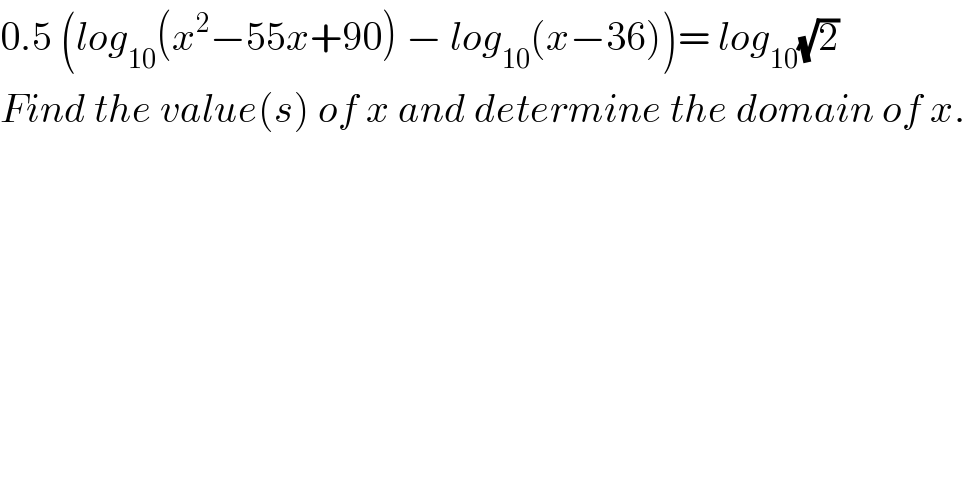
0.5 (log_(10) (x^2 −55x+90) − log_(10) (x−36))= log_(10) (√2) Find the value(s) of x and determine the domain of x.
$$\mathrm{0}.\mathrm{5}\:\left({log}_{\mathrm{10}} \left({x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}\right)\:−\:{log}_{\mathrm{10}} \left({x}−\mathrm{36}\right)\right)=\:{log}_{\mathrm{10}} \sqrt{\mathrm{2}} \\ $$$${Find}\:{the}\:{value}\left({s}\right)\:{of}\:{x}\:{and}\:{determine}\:{the}\:{domain}\:{of}\:{x}. \\ $$
Commented by Yozzii last updated on 29/Jan/16
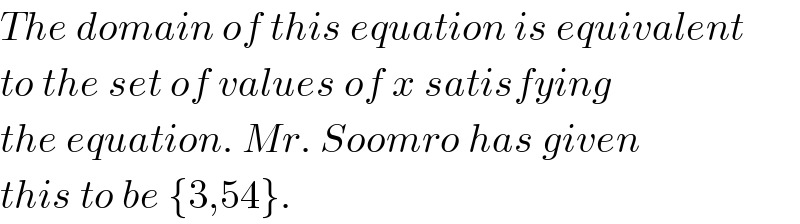
The domain of this equation is equivalent to the set of values of x satisfying the equation. Mr. Soomro has given this to be {3,54}.
$${The}\:{domain}\:{of}\:{this}\:{equation}\:{is}\:{equivalent} \\ $$$${to}\:{the}\:{set}\:{of}\:{values}\:{of}\:{x}\:{satisfying} \\ $$$${the}\:{equation}.\:{Mr}.\:{Soomro}\:{has}\:{given} \\ $$$${this}\:{to}\:{be}\:\left\{\mathrm{3},\mathrm{54}\right\}. \\ $$
Answered by Rasheed Soomro last updated on 29/Jan/16
0.5 (log_(10) (x^2 −55x+90) − log_(10) (x−36))= log_(10) (√2) log_(10) (x^2 −55x+90)^(1/2) − log_(10) (x−36)^(1/2) = log_(10) 2^(1/2) log_(10) (((x^2 −55x+90)/(x−36)))^(1/2) =log_(10) 2^(1/2) (((x^2 −55x+90)/(x−36)))^(1/2) =2^(1/2) ((x^2 −55x+90)/(x−36))=2 x^2 −55x+90−2x+72=0 x^2 −57x+162=0 x^2 −54x−3x+162=0 x(x−54)−3(x−54)=0 (x−54)(x−3)=0 x=3 ∣ x=54 If f(x)=0.5 (log_(10) (x^2 −55x+90) − log_(10) (x−36))− log_(10) (√2) For real f(x) x^2 −55x+90>0 ∧ x−36>0 x−36>0 ⇒ x>36........................................(i) Equation x^2 −55x+90=0 has two solutions x=((55+(√(2665)))/2),((55+(√(2665)))/2) So inequality x^2 −55x+90>0 has solutions: x>((55+(√(2665)))/2)≈53.31 ,x>((55−(√(2665)))/2) ≈1.69 .......(ii) Domain is intersection of (i) & (ii) {x : x∈R ∧ x>((55+(√(2665)))/2)≈53.31}
$$\mathrm{0}.\mathrm{5}\:\left({log}_{\mathrm{10}} \left({x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}\right)\:−\:{log}_{\mathrm{10}} \left({x}−\mathrm{36}\right)\right)=\:{log}_{\mathrm{10}} \sqrt{\mathrm{2}} \\ $$$${log}_{\mathrm{10}} \left({x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}\right)^{\mathrm{1}/\mathrm{2}} \:−\:{log}_{\mathrm{10}} \left({x}−\mathrm{36}\right)^{\mathrm{1}/\mathrm{2}} =\:{log}_{\mathrm{10}} \mathrm{2}^{\mathrm{1}/\mathrm{2}} \\ $$$${log}_{\mathrm{10}} \left(\frac{{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}}{{x}−\mathrm{36}}\right)^{\mathrm{1}/\mathrm{2}} ={log}_{\mathrm{10}} \mathrm{2}^{\mathrm{1}/\mathrm{2}} \\ $$$$\left(\frac{{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}}{{x}−\mathrm{36}}\right)^{\mathrm{1}/\mathrm{2}} =\mathrm{2}^{\mathrm{1}/\mathrm{2}} \\ $$$$\frac{{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}}{{x}−\mathrm{36}}=\mathrm{2} \\ $$$${x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}−\mathrm{2}{x}+\mathrm{72}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{57}{x}+\mathrm{162}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} −\mathrm{54}{x}−\mathrm{3}{x}+\mathrm{162}=\mathrm{0} \\ $$$${x}\left({x}−\mathrm{54}\right)−\mathrm{3}\left({x}−\mathrm{54}\right)=\mathrm{0} \\ $$$$\left({x}−\mathrm{54}\right)\left({x}−\mathrm{3}\right)=\mathrm{0} \\ $$$${x}=\mathrm{3}\:\mid\:{x}=\mathrm{54} \\ $$$$ \\ $$$${If}\:{f}\left({x}\right)=\mathrm{0}.\mathrm{5}\:\left({log}_{\mathrm{10}} \left({x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}\right)\:−\:{log}_{\mathrm{10}} \left({x}−\mathrm{36}\right)\right)−\:{log}_{\mathrm{10}} \sqrt{\mathrm{2}} \\ $$$${For}\:{real}\:{f}\left({x}\right)\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}>\mathrm{0}\:\:\wedge\:{x}−\mathrm{36}>\mathrm{0} \\ $$$${x}−\mathrm{36}>\mathrm{0}\:\Rightarrow\:{x}>\mathrm{36}………………………………….\left({i}\right) \\ $$$${Equation}\:{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}=\mathrm{0}\:{has}\:{two}\:{solutions} \\ $$$${x}=\frac{\mathrm{55}+\sqrt{\mathrm{2665}}}{\mathrm{2}},\frac{\mathrm{55}+\sqrt{\mathrm{2665}}}{\mathrm{2}} \\ $$$${So}\:{inequality}\:\:{x}^{\mathrm{2}} −\mathrm{55}{x}+\mathrm{90}>\mathrm{0}\:{has}\:{solutions}: \\ $$$${x}>\frac{\mathrm{55}+\sqrt{\mathrm{2665}}}{\mathrm{2}}\approx\mathrm{53}.\mathrm{31}\:\:,{x}>\frac{\mathrm{55}−\sqrt{\mathrm{2665}}}{\mathrm{2}}\:\approx\mathrm{1}.\mathrm{69}\:…….\left({ii}\right) \\ $$$$\mathrm{Domain}\:\mathrm{is}\:{intersection}\:{of}\:\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left\{\mathrm{x}\::\:{x}\in\mathbb{R}\:\wedge\:{x}>\frac{\mathrm{55}+\sqrt{\mathrm{2665}}}{\mathrm{2}}\approx\mathrm{53}.\mathrm{31}\right\} \\ $$$$\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *