Question Number 77087 by Dah Solu Tion last updated on 03/Jan/20

$$\int_{\mathrm{0}} ^{\frac{\boldsymbol{{a}}}{\mathrm{2}}} \boldsymbol{{x}}^{\mathrm{2}} \left(\boldsymbol{{a}}^{\mathrm{2}} −\boldsymbol{{x}}^{\mathrm{2}} \right)^{\frac{−\mathrm{3}}{\mathrm{2}}} \boldsymbol{{dx}} \\ $$$$\boldsymbol{{Help}}!!! \\ $$$$ \\ $$
Commented by turbo msup by abdo last updated on 03/Jan/20
![changement x=asint give ∫_0 ^(a/2) x^2 (a^2 −x^2 )^(−(3/2)) dx =∫_0 ^(π/6) a^2 sin^2 t ×a^(−3) (1−sin^2 t)^(−(3/2)) acos t dt =∫_0 ^(π/6) sin^2 t×(cost)^(−3) cost dt =∫_0 ^(π/6) tan^2 t dt =∫_0 ^(π/6) (1+tan^2 t−1)dt =∫_0 ^(π/6) (1+tan^2 t)dt−(π/6) =[tant]_0 ^(π/6) −(π/6) =(1/( (√3)))−(π/6)](https://www.tinkutara.com/question/Q77113.png)
$${changement}\:{x}={asint}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\frac{{a}}{\mathrm{2}}} \:{x}^{\mathrm{2}} \left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:{a}^{\mathrm{2}} \:{sin}^{\mathrm{2}} {t}\:×{a}^{−\mathrm{3}} \left(\mathrm{1}−{sin}^{\mathrm{2}} {t}\right)^{−\frac{\mathrm{3}}{\mathrm{2}}} \:{acos}\:{t}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:{sin}^{\mathrm{2}} {t}×\left({cost}\right)^{−\mathrm{3}} \:{cost}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\:{tan}^{\mathrm{2}} {t}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\left(\mathrm{1}+{tan}^{\mathrm{2}} {t}−\mathrm{1}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {t}\right){dt}−\frac{\pi}{\mathrm{6}} \\ $$$$=\left[{tant}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} −\frac{\pi}{\mathrm{6}}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{6}} \\ $$
Answered by john santu last updated on 03/Jan/20
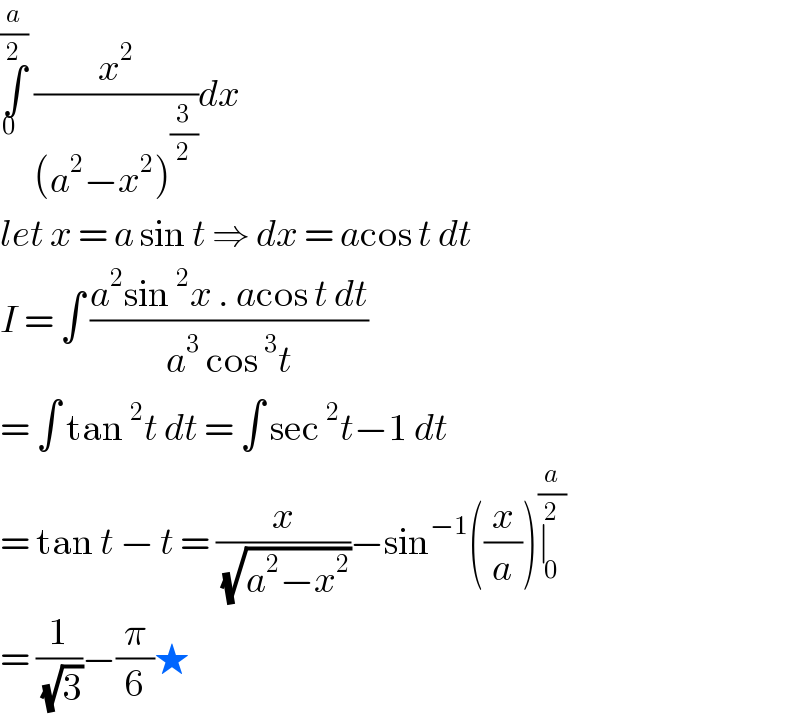
$$\underset{\mathrm{0}\:\:} {\overset{\frac{{a}}{\mathrm{2}}} {\int}}\:\frac{{x}^{\mathrm{2}} }{\left({a}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{dx}\: \\ $$$${let}\:{x}\:=\:{a}\:\mathrm{sin}\:{t}\:\Rightarrow\:{dx}\:=\:{a}\mathrm{cos}\:{t}\:{dt}\: \\ $$$${I}\:=\:\int\:\frac{{a}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} {x}\:.\:{a}\mathrm{cos}\:{t}\:{dt}}{{a}^{\mathrm{3}} \:\mathrm{cos}\:^{\mathrm{3}} {t}} \\ $$$$=\:\int\:\mathrm{tan}\:^{\mathrm{2}} {t}\:{dt}\:=\:\int\:\mathrm{sec}\:^{\mathrm{2}} {t}−\mathrm{1}\:{dt} \\ $$$$=\:\mathrm{tan}\:{t}\:−\:{t}\:=\:\frac{{x}}{\:\sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} }}−\mathrm{sin}^{−\mathrm{1}} \left(\frac{{x}}{{a}}\right)\underset{\mathrm{0}} {\overset{\frac{{a}}{\mathrm{2}}} {\mid}} \\ $$$$=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{6}}\bigstar \\ $$
