Question Number 135824 by Khakie last updated on 16/Mar/21

$$\int_{\mathrm{0}} ^{{a}} \:\frac{{x}^{\mathrm{4}} \:\:{e}^{{x}} }{\left({e}^{{x}} \:−\mathrm{1}\right)^{\mathrm{2}} }\:{dt} \\ $$$$ \\ $$$${please}\:{solve}\:{this}… \\ $$
Commented by mathmax by abdo last updated on 16/Mar/21
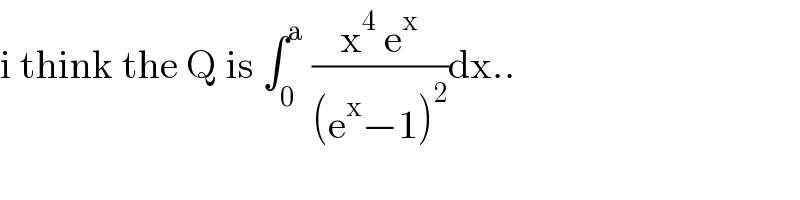
$$\mathrm{i}\:\mathrm{think}\:\mathrm{the}\:\mathrm{Q}\:\mathrm{is}\:\int_{\mathrm{0}} ^{\mathrm{a}} \:\frac{\mathrm{x}^{\mathrm{4}} \:\mathrm{e}^{\mathrm{x}} }{\left(\mathrm{e}^{\mathrm{x}} −\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}.. \\ $$
Answered by Ñï= last updated on 16/Mar/21
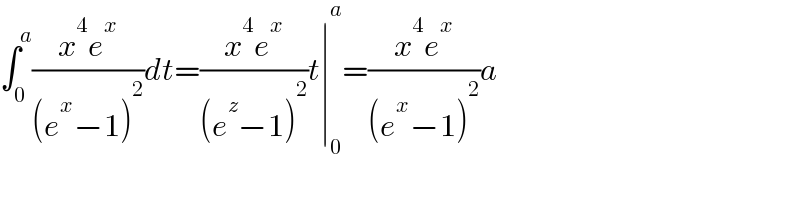
$$\int_{\mathrm{0}} ^{{a}} \frac{{x}^{\mathrm{4}} {e}^{{x}} }{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }{dt}=\frac{{x}^{\mathrm{4}} {e}^{{x}} }{\left({e}^{{z}} −\mathrm{1}\right)^{\mathrm{2}} }{t}\mid_{\mathrm{0}} ^{{a}} =\frac{{x}^{\mathrm{4}} {e}^{{x}} }{\left({e}^{{x}} −\mathrm{1}\right)^{\mathrm{2}} }{a} \\ $$
