Question Number 134418 by mnjuly1970 last updated on 03/Mar/21
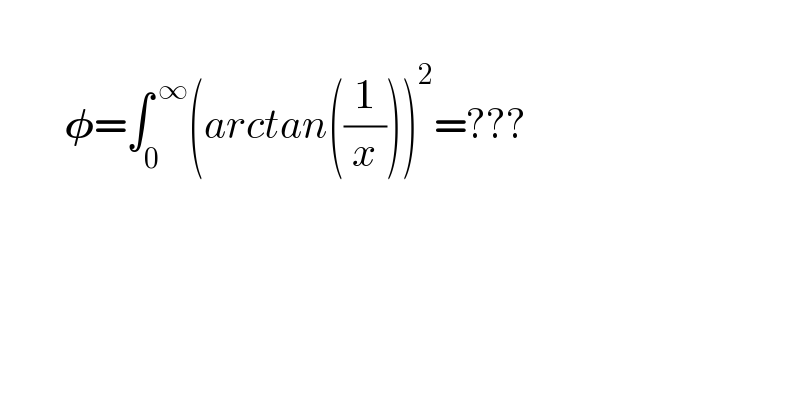
$$ \\ $$$$\:\:\:\:\:\:\:\:\boldsymbol{\phi}=\int_{\mathrm{0}} ^{\:\infty} \left({arctan}\left(\frac{\mathrm{1}}{{x}}\right)\right)^{\mathrm{2}} =??? \\ $$
Answered by Ñï= last updated on 03/Mar/21
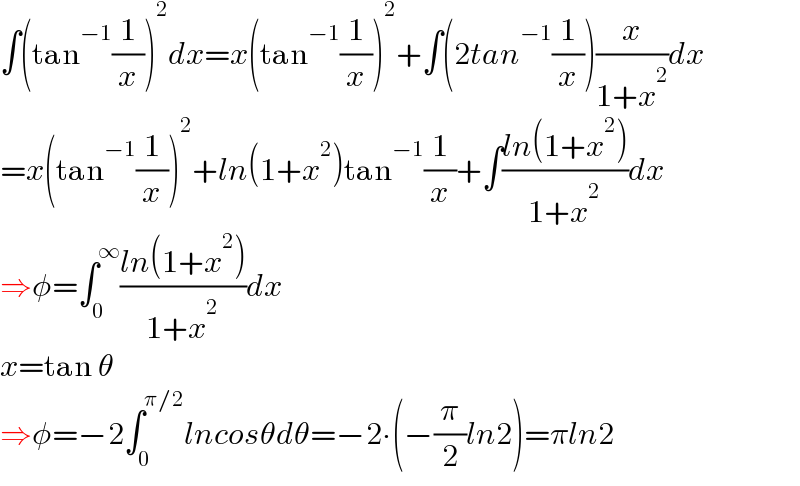
$$\int\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} {dx}={x}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\int\left(\mathrm{2}{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right)\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$={x}\left(\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{{x}}+\int\frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$\Rightarrow\phi=\int_{\mathrm{0}} ^{\infty} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${x}=\mathrm{tan}\:\theta \\ $$$$\Rightarrow\phi=−\mathrm{2}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} {lncos}\theta{d}\theta=−\mathrm{2}\centerdot\left(−\frac{\pi}{\mathrm{2}}{ln}\mathrm{2}\right)=\pi{ln}\mathrm{2} \\ $$
Commented by mnjuly1970 last updated on 03/Mar/21
$${thank}\:{you}\:{so}\:{much}.. \\ $$
