Menu Close

0-dx-x-4-x-2-1-2-

Tinku Tara 0 Comments
Pin




Question Number 132410 by bramlexs22 last updated on 14/Feb/21
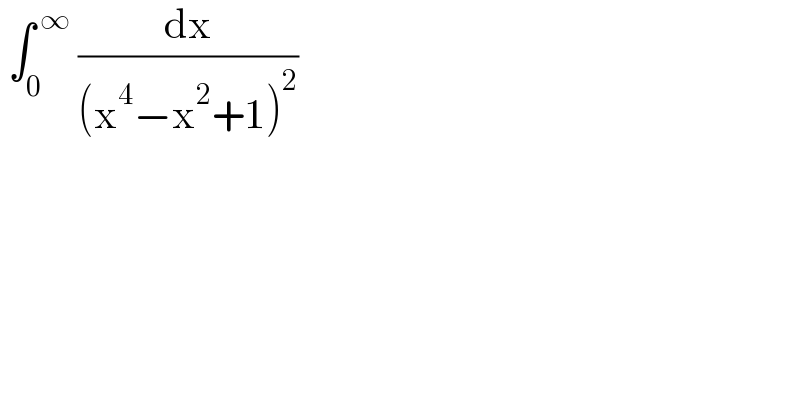
∫_0 ^( ∞) (dx/((x^4 −x^2 +1)^2 ))
$$\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\: \\ $$
Answered by EDWIN88 last updated on 14/Feb/21
I=∫_0 ^∞ (dx/((x^4 −x^2 +1))) ; replace x by (1/x) I=∫_∞ ^0 (((−(1/x^2 ))/(((1/x^4 )−(1/x^2 )+1)^2 )))dx=∫_0 ^∞ ((x^6 dx)/((x^4 −x^2 +1)^2 )) 2I=∫_0 ^∞ ((x^6 +1)/((x^4 −x^2 +1)^2 ))dx ; Q(x)=(x^4 −x^2 +1)^2 Q′(x)=2(4x^3 −2x)(x^4 −x^2 +1) gcd Q′(x) and Q(x) is Q_1 (x)=x^4 −x^2 +1 and Q_2 (x)=((Q(x))/(Q_1 (x)))= x^4 −x^2 +1 I=(1/2)∫((x^6 +1)/((x^4 −x^2 +1)^2 )) dx = (1/2){ [((ax^3 +bx^2 +cx+d)/(x^4 −x^2 +1)) ]+∫ ((ex^3 +fx^2 +gx+h)/(x^4 −x^2 +1)) dx } differentiating both sides and solving for coefficients
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)}\:;\:\mathrm{replace}\:\mathrm{x}\:\mathrm{by}\:\frac{\mathrm{1}}{\mathrm{x}} \\ $$$$\mathrm{I}=\int_{\infty} ^{\mathrm{0}} \:\left(\frac{−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }}{\left(\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{4}} }−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }+\mathrm{1}\right)^{\mathrm{2}} }\right)\mathrm{dx}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{x}^{\mathrm{6}} \:\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:;\:\mathrm{Q}\left(\mathrm{x}\right)=\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\mathrm{Q}'\left(\mathrm{x}\right)=\mathrm{2}\left(\mathrm{4x}^{\mathrm{3}} −\mathrm{2x}\right)\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{gcd}\:\mathrm{Q}'\left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{Q}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{Q}_{\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{Q}_{\mathrm{2}} \left(\mathrm{x}\right)=\frac{\mathrm{Q}\left(\mathrm{x}\right)}{\mathrm{Q}_{\mathrm{1}} \left(\mathrm{x}\right)}=\:\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1} \\ $$$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{x}^{\mathrm{6}} +\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left[\frac{\mathrm{ax}^{\mathrm{3}} +\mathrm{bx}^{\mathrm{2}} +\mathrm{cx}+\mathrm{d}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\right]+\int\:\frac{\mathrm{ex}^{\mathrm{3}} +\mathrm{fx}^{\mathrm{2}} +\mathrm{gx}+\mathrm{h}}{\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:\mathrm{dx}\:\right\} \\ $$$$\mathrm{differentiating}\:\mathrm{both}\:\mathrm{sides}\:\mathrm{and}\:\mathrm{solving}\: \\ $$$$\mathrm{for}\:\mathrm{coefficients}\: \\ $$$$ \\ $$
Answered by Lordose last updated on 14/Feb/21
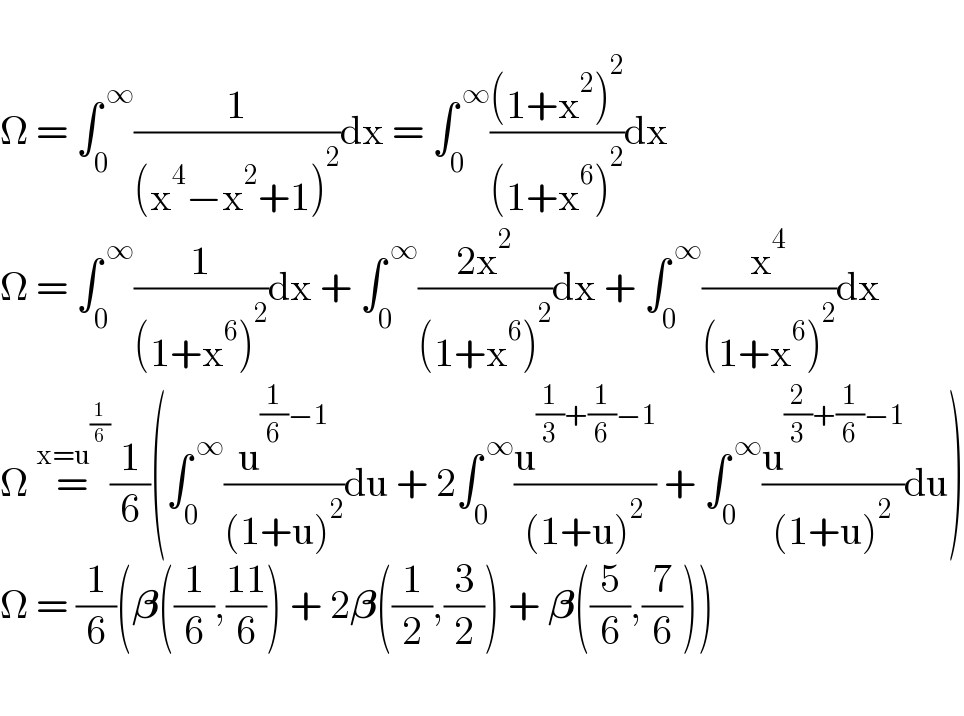
Ω = ∫_0 ^( ∞) (1/((x^4 −x^2 +1)^2 ))dx = ∫_0 ^( ∞) (((1+x^2 )^2 )/((1+x^6 )^2 ))dx Ω = ∫_0 ^( ∞) (1/((1+x^6 )^2 ))dx + ∫_0 ^( ∞) ((2x^2 )/((1+x^6 )^2 ))dx + ∫_0 ^( ∞) (x^4 /((1+x^6 )^2 ))dx Ω =^(x=u^(1/6) ) (1/6)(∫_0 ^( ∞) (u^((1/6)−1) /((1+u)^2 ))du + 2∫_0 ^( ∞) (u^((1/3)+(1/6)−1) /((1+u)^2 )) + ∫_0 ^( ∞) (u^((2/3)+(1/6)−1) /((1+u)^2 ))du) Ω = (1/6)(𝛃((1/6),((11)/6)) + 2𝛃((1/2),(3/2)) + 𝛃((5/6),(7/6)))
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{2x}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx}\:+\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{x}^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{6}} \right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{x}=\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}} } {=}\frac{\mathrm{1}}{\mathrm{6}}\left(\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}\:+\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\:+\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{u}^{\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\mathrm{du}\right) \\ $$$$\Omega\:=\:\frac{\mathrm{1}}{\mathrm{6}}\left(\boldsymbol{\beta}\left(\frac{\mathrm{1}}{\mathrm{6}},\frac{\mathrm{11}}{\mathrm{6}}\right)\:+\:\mathrm{2}\boldsymbol{\beta}\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\:+\:\boldsymbol{\beta}\left(\frac{\mathrm{5}}{\mathrm{6}},\frac{\mathrm{7}}{\mathrm{6}}\right)\right) \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 14/Feb/21
∫_0 ^∞ (((x^2 +1)^2 )/((x^6 +1)^2 ))dx=∫_0 ^∞ (x^4 /((x^6 +1)^2 ))dx+((2x^2 )/((x^6 +1)^2 ))+(1/((x^6 +1)^2 ))dx x^6 =u =(1/6)∫_0 ^∞ (u^(−(1/6)) /((u+1)^2 ))du+(1/3)∫_0 ^∞ (u^(−(1/2)) /((u+1)^2 ))+(1/6)∫_0 ^∞ (u^(−(5/(6 )) ) /((u+1)^2 ))du =(1/6)∫_0 ^∞ (u^((5/6)−1) /((u+1)^((7/6)+(5/6)) ))+(1/3)∫_0 ^∞ (u^((1/2)−1) /((u+1)^((3/2)+(1/2)) ))+(1/6)∫_0 ^∞ (u^((1/6)−1) /((u+1)^((1/6)+((11)/6)) ))du =(1/6).((Γ((5/6))Γ((7/6)))/(Γ(2)))+(1/3).((Γ((1/2))Γ((3/2)))/(Γ(2)))+(1/6).((Γ((1/6))Γ(((11)/6)))/(Γ(2))) =(π/(18))+(π/6)+((5π)/(18))=(π/2)
$$\int_{\mathrm{0}} ^{\infty} \frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{4}} }{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({x}^{\mathrm{6}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:\:\:\:{x}^{\mathrm{6}} ={u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{6}}} }{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{du}+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{−\frac{\mathrm{5}}{\mathrm{6}\:}\:\:\:\:} }{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{5}}{\mathrm{6}}−\mathrm{1}} }{\left({u}+\mathrm{1}\right)^{\frac{\mathrm{7}}{\mathrm{6}}+\frac{\mathrm{5}}{\mathrm{6}}} }+\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left({u}+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}} }+\frac{\mathrm{1}}{\mathrm{6}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{\mathrm{6}}−\mathrm{1}} }{\left({u}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{11}}{\mathrm{6}}} }{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}.\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{7}}{\mathrm{6}}\right)}{\Gamma\left(\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{3}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{2}\right)}+\frac{\mathrm{1}}{\mathrm{6}}.\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\Gamma\left(\frac{\mathrm{11}}{\mathrm{6}}\right)}{\Gamma\left(\mathrm{2}\right)} \\ $$$$=\frac{\pi}{\mathrm{18}}+\frac{\pi}{\mathrm{6}}+\frac{\mathrm{5}\pi}{\mathrm{18}}=\frac{\pi}{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 14/Feb/21
I=∫_0 ^∞ (dx/((x^4 −x^2 +1)^2 )) ⇒2I=∫_(−∞) ^(+∞) (dx/((x^4 −x^2 +1)^2 )) ϕ(z)=(1/((z^4 −z^2 +1)^2 )) poles of ϕ! z^4 −z^2 +1=0 ⇒u^2 −u+1=0(u=z^2 ) Δ=−3 ⇒u_1 =((1+i(√3))/2) =e^((iπ)/3) and u_2 =e^(−((iπ)/3)) ⇒ z^4 −z^2 +1 =(z^2 −e^((iπ)/3) )(z^2 −e^(−((iπ)/3)) ) ⇒ϕ(z)=(1/((z^2 −e^((iπ)/3) )^2 (z^2 −e^(−((iπ)/3)) )^2 )) =(1/((z−e^((iπ)/6) )^2 (z+e^((iπ)/6) )^2 (z−e^(−((iπ)/6)) )^2 (z+e^(−((iπ)/6)) )^2 )) the poles of ϕ are +^− e^((iπ)/6) and +^− e^(−((iπ)/6)) (doubles) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/6) )+Res(ϕ,−e^(−((iπ)/6)) )} Res(ϕ,e^((iπ)/6) )=lim_(z→e^((iπ)/6) ) (1/((2−1)!)){(z−e^((iπ)/6) )^2 ϕ(z)}^((1)) =lim_(z→e^((iπ)/6) ) {(1/((z+e^((iπ)/6) )^2 (z^2 −e^(−((iπ)/3)) )))}^((1)) =lim_(z→e^((iπ)/6) ) −((2(z+e^((iπ)/6) )(z^2 −e^(−((iπ)/3)) )+2z(z+e^((iπ)/6) )^2 )/((z+e^((iπ)/6) )^4 (z^2 −e^(−((iπ)/3)) )^4 )) =−lim_(z→e^((iπ)/6) ) (2/((z+e^((iπ)/6) )^3 (z^2 −e^(−((iπ)/3)) )^3 )) +((2z)/((z+e^((iπ)/6) )^2 (z^2 −e^(−((iπ)/3)) )^4 )) =−{(2/((2e^((iπ)/3) )^3 (2isin((π/3)))^3 )) +((2e^((iπ)/6) )/((2e^((iπ)/6) )^2 (2isin((π/3)))^4 ))} =−{(2/(8(−1)(−8i)(((√3)/2))^3 )) +((2e^((iπ)/6) )/(4e^((iπ)/3) .16(((√3)/2))^4 ))}....be continued...
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{2I}=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{4}} −\mathrm{z}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{poles}\:\mathrm{of}\:\varphi! \\ $$$$\mathrm{z}^{\mathrm{4}} −\mathrm{z}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}=\mathrm{0}\left(\mathrm{u}=\mathrm{z}^{\mathrm{2}} \right) \\ $$$$\Delta=−\mathrm{3}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{z}^{\mathrm{4}} −\mathrm{z}^{\mathrm{2}} +\mathrm{1}\:=\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)\:\Rightarrow\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} } \\ $$$$\mathrm{the}\:\mathrm{poles}\:\mathrm{of}\:\varphi\:\mathrm{are}\:\overset{−} {+}\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \:\mathrm{and}\:\overset{−} {+}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \:\:\left(\mathrm{doubles}\right) \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\:\left\{\frac{\mathrm{1}}{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)}\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\:−\frac{\mathrm{2}\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)+\mathrm{2z}\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} }{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} } \\ $$$$=−\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\frac{\mathrm{2}}{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} }\:+\frac{\mathrm{2z}}{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{4}} } \\ $$$$=−\left\{\frac{\mathrm{2}}{\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} \left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)^{\mathrm{3}} }\:+\frac{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} }{\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{2isin}\left(\frac{\pi}{\mathrm{3}}\right)\right)^{\mathrm{4}} }\right\} \\ $$$$=−\left\{\frac{\mathrm{2}}{\mathrm{8}\left(−\mathrm{1}\right)\left(−\mathrm{8i}\right)\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{3}} }\:+\frac{\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} }{\mathrm{4e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} .\mathrm{16}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{4}} }\right\}….\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *