Menu Close

0-dx-x-4-x-2-1-3-

Tinku Tara 0 Comments
Pin




Question Number 141407 by mnjuly1970 last updated on 18/May/21
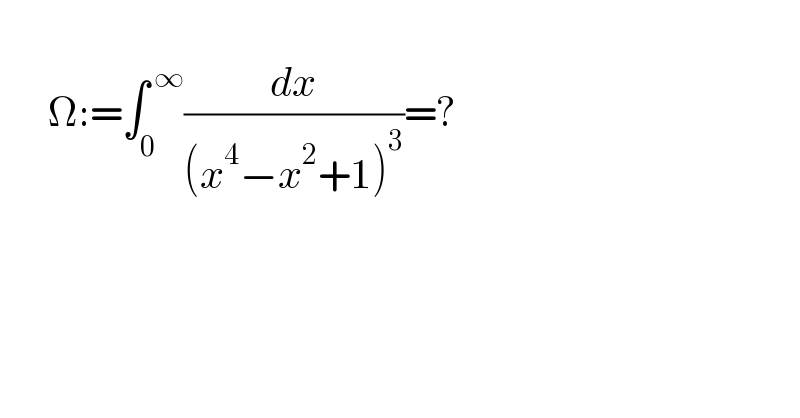
Ω:=∫_0 ^( ∞) (dx/((x^4 −x^2 +1)^3 ))=?
$$ \\ $$$$\:\:\:\:\:\:\Omega:=\int_{\mathrm{0}} ^{\:\infty} \frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }=? \\ $$
Answered by MJS_new last updated on 18/May/21
∫(dx/((x^4 −x^2 +1)^3 ))= [Ostrogradski′s Method] =((x(7x^6 −5x^4 +7x^2 +4))/(24(x^4 −x^2 +1)^2 ))+(1/(24))∫((7x^2 +20)/(x^4 −x^2 +1))dx (1/(24))∫((7x^2 +20)/(x^4 −x^2 +1))dx= =−((13(√3))/(288))∫((2x−(√3))/(x^2 −(√3)x+1))dx+(9/(32))∫(dx/(x^2 −(√3)x+1))+((13(√3))/(288))∫((2x+(√3))/(x^2 +(√3)x+1))dx+(9/(32))∫(dx/(x^2 +(√3)x+1))= ... =((13(√3))/(288))ln ((x^2 +(√3)x+1)/(x^2 −(√3)x+1)) +(9/(16))(arctan (2x−(√3)) +arctan (2x+(√3))) +C ⇒ answer is ((9π)/(16))
$$\int\frac{{dx}}{\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{x}\left(\mathrm{7}{x}^{\mathrm{6}} −\mathrm{5}{x}^{\mathrm{4}} +\mathrm{7}{x}^{\mathrm{2}} +\mathrm{4}\right)}{\mathrm{24}\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{24}}\int\frac{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{20}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{24}}\int\frac{\mathrm{7}{x}^{\mathrm{2}} +\mathrm{20}}{{x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$=−\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{288}}\int\frac{\mathrm{2}{x}−\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{9}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}+\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{288}}\int\frac{\mathrm{2}{x}+\sqrt{\mathrm{3}}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{dx}+\frac{\mathrm{9}}{\mathrm{32}}\int\frac{{dx}}{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}= \\ $$$$… \\ $$$$=\frac{\mathrm{13}\sqrt{\mathrm{3}}}{\mathrm{288}}\mathrm{ln}\:\frac{{x}^{\mathrm{2}} +\sqrt{\mathrm{3}}{x}+\mathrm{1}}{{x}^{\mathrm{2}} −\sqrt{\mathrm{3}}{x}+\mathrm{1}}\:+\frac{\mathrm{9}}{\mathrm{16}}\left(\mathrm{arctan}\:\left(\mathrm{2}{x}−\sqrt{\mathrm{3}}\right)\:+\mathrm{arctan}\:\left(\mathrm{2}{x}+\sqrt{\mathrm{3}}\right)\right)\:+{C} \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{9}\pi}{\mathrm{16}} \\ $$
Commented by mnjuly1970 last updated on 18/May/21
thank you mr m j s
$${thank}\:{you}\:{mr}\:{m}\:{j}\:\:{s} \\ $$
Answered by mathmax by abdo last updated on 19/May/21
Φ=(1/2)∫_(−∞) ^(+∞) (dx/((x^4 −x^2 +1)^3 )) let ϕ(z)=(1/((z^4 −z^2 +1)^3 )) poles of ϕ? z^4 −z^2 +1=0 ⇒u^2 −u+1=0 (z^2 =u) Δ=−3 ⇒u_1 =((1+i(√3))/2) =e^((iπ)/3) and u_2 =((1−i(√3))/2)=e^(−((iπ)/3)) ϕ(z)=(1/((z^2 −e^((iπ)/3) )^3 (z^2 −e^(−((iπ)/3)) )^3 )) =(1/((z−e^((iπ)/6) )^3 (z+e^((iπ)/6) )^3 (z−e^(−((iπ)/6)) )^3 (z+e^(−((iπ)/6)) )^3 )) ∫_R ϕ(z)dz =2iπ{ Res(ϕ,e^((iπ)/6) ) +Res(ϕ,−e^(−((iπ)/6)) )} Res(ϕ ,e^((iπ)/6) ) =lim_(z→e^((iπ)/6) ) (1/((3−1)!)){(z−e^((iπ)/6) )^3 ϕ(z)}^((2)) =lim_(z→e^((iπ)/6) ) (1/2)((1/((z+e^((iπ)/6) )^3 (z^2 −e^(−((iπ)/6)) )^3 )))^((2)) =lim_(z→e^((iπ)/6) ) − (1/2)×((3(z+e^((iπ)/6) )^2 (z^2 −e^(−((iπ)/6)) )^3 +3(z+e^((iπ)/6) )^3 (2z)(z^2 −e^(−((iπ)/6)) )^2 )/((z+e^((iπ)/6) )^6 (z^2 −e^(−((iπ)/6)) )^6 )) =−(1/2)lim_(z→e^((iπ)/6) ) ((3(z^2 −e^(−((iπ)/6)) )+6z(z+e^((iπ)/6) ))/((z+e^((iπ)/6) )^4 (z^2 −e^(−((iπ)/6)) )^4 )) =−(1/2).((3(e^((iπ)/3) −e^(−((iπ)/6)) )+6e^((iπ)/6) (2e^((iπ)/6) ))/((2e^((iπ)/6) )^4 (e^((iπ)/3) −e^(−((iπ)/6)) )^4 ))....be continued...
$$\Phi=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{x}^{\mathrm{4}} −\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\:\mathrm{let}\:\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{4}} −\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{3}} }\:\mathrm{poles}\:\mathrm{of}\:\varphi? \\ $$$$\mathrm{z}^{\mathrm{4}} −\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}=\mathrm{0}\:\Rightarrow\mathrm{u}^{\mathrm{2}} −\mathrm{u}+\mathrm{1}=\mathrm{0}\:\:\left(\mathrm{z}^{\mathrm{2}} =\mathrm{u}\right) \\ $$$$\Delta=−\mathrm{3}\:\Rightarrow\mathrm{u}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:=\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{u}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \\ $$$$\varphi\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \right)^{\mathrm{3}} }\:=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{z}−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{z}+\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} } \\ $$$$\int_{\mathrm{R}} \varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\left\{\:\mathrm{Res}\left(\varphi,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)\:+\mathrm{Res}\left(\varphi,−\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)\right\} \\ $$$$\mathrm{Res}\left(\varphi\:,\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)\:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\frac{\mathrm{1}}{\left(\mathrm{3}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \:\varphi\left(\mathrm{z}\right)\right\}^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} }\right)^{\left(\mathrm{2}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:−\:\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \:+\mathrm{3}\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{3}} \left(\mathrm{2z}\right)\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{2}} }{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{6}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{6}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} } \:\:\:\:\frac{\mathrm{3}\left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)+\mathrm{6z}\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)}{\left(\mathrm{z}+\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} \left(\mathrm{z}^{\mathrm{2}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} } \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{3}\left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)+\mathrm{6e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)}{\left(\mathrm{2e}^{\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} \left(\mathrm{e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} −\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{6}}} \right)^{\mathrm{4}} }….\mathrm{be}\:\mathrm{continued}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *