Question Number 143622 by ArielVyny last updated on 16/Jun/21
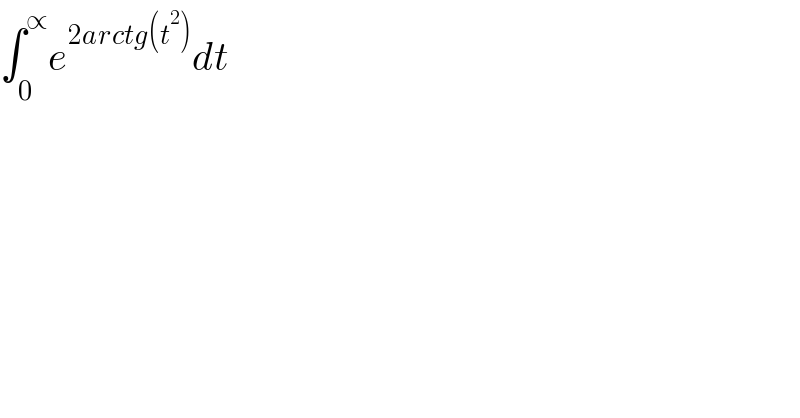
$$\int_{\mathrm{0}} ^{\propto} {e}^{\mathrm{2}{arctg}\left({t}^{\mathrm{2}} \right)} {dt} \\ $$
Answered by TheHoneyCat last updated on 17/Jun/21

$$\mathrm{arctan}\left({t}\right)\underset{{t}\rightarrow+\infty} {\rightarrow}\frac{\pi}{\mathrm{2}}>\mathrm{0} \\ $$$$\mathrm{so}\:{e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} \underset{{t}\rightarrow+\infty} {\rightarrow}{e}^{\pi} >{e}^{\mathrm{3}} >{e}>\mathrm{1} \\ $$$$\mathrm{thus}\:\exists\mathrm{X}\in\mathbb{R}_{+} \mid\:\forall{x}\in\left[{x},+\infty\left[\:{e}^{\mathrm{2arctan}\left({x}^{\mathrm{2}} \right)} >\mathrm{1}\right.\right. \\ $$$$\mathrm{let}\:\mathrm{X}\:\:\mathrm{be}\:\mathrm{such}\:\mathrm{a}\:\mathrm{real}\:\mathrm{number} \\ $$$$\int_{\mathrm{0}} ^{+\infty} {e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} {dt}=\int_{\mathrm{0}} ^{\mathrm{X}} {e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} {dt}\:+\:\int_{\mathrm{X}} ^{+\infty} {e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} {dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{X}} {e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} {dt}\:\in\mathbb{R}\:\mathrm{as}\:\mathrm{the}\:\mathrm{integral}\:\mathrm{of}\:\mathrm{a}\:\mathrm{Continued}\:\mathrm{function}\:\mathrm{on}\:\mathrm{a}\:\mathrm{segment} \\ $$$$\int_{\mathrm{X}} ^{+\infty} {e}^{\mathrm{2arctan}\left({t}^{\mathrm{2}} \right)} {dt}\:\geqslant\:\int_{\mathrm{X}} ^{+\infty} {dt}=\mathrm{lim}_{{x}\rightarrow+\infty} \left({x}−\mathrm{X}\right)=+\infty \\ $$$$ \\ $$$$\mathrm{in}\:\mathrm{a}\:\mathrm{word}:\:\int_{\mathrm{0}} ^{+\infty} {e}^{\mathrm{2artcan}\left({t}^{\mathrm{2}} \right)} {dt}=+\infty\:_{\blacksquare} \\ $$$$ \\ $$$${perhaps}\:{you}\:{made}\:{a}\:{mistake}\:{when}\:{writting}\:{it}… \\ $$
