Question Number 1571 by 112358 last updated on 20/Aug/15
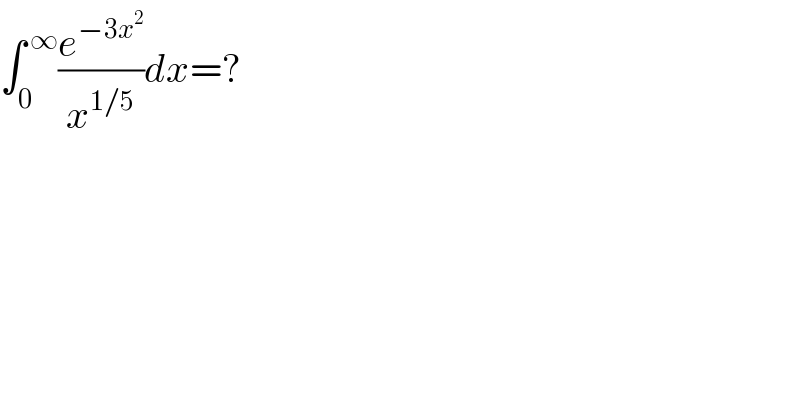
$$\int_{\mathrm{0}} ^{\:\infty} \frac{{e}^{−\mathrm{3}{x}^{\mathrm{2}} } }{{x}^{\mathrm{1}/\mathrm{5}} }{dx}=? \\ $$
Answered by prakash jain last updated on 20/Aug/15
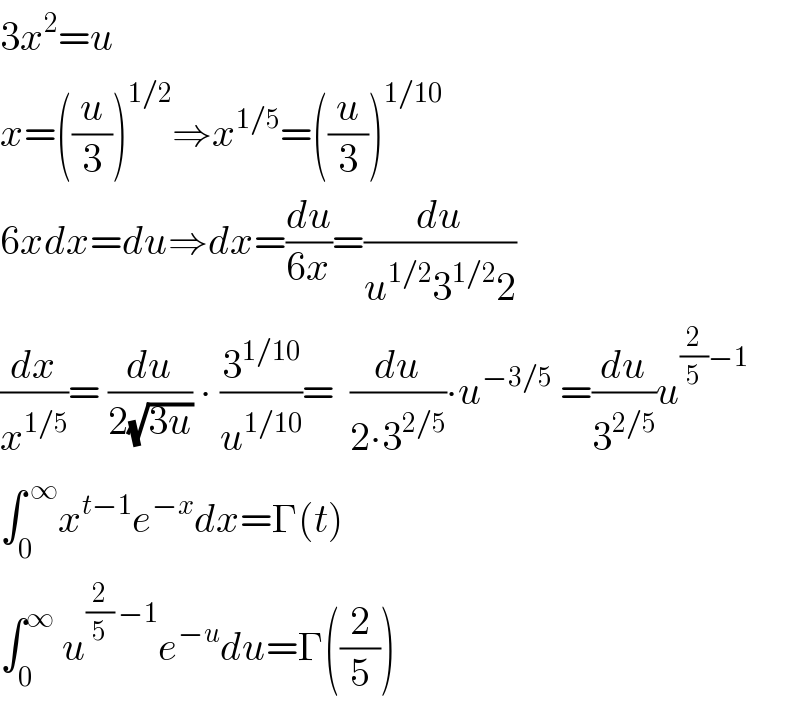
$$\mathrm{3}{x}^{\mathrm{2}} ={u} \\ $$$${x}=\left(\frac{{u}}{\mathrm{3}}\right)^{\mathrm{1}/\mathrm{2}} \Rightarrow{x}^{\mathrm{1}/\mathrm{5}} =\left(\frac{{u}}{\mathrm{3}}\right)^{\mathrm{1}/\mathrm{10}} \\ $$$$\mathrm{6}{xdx}={du}\Rightarrow{dx}=\frac{{du}}{\mathrm{6}{x}}=\frac{{du}}{{u}^{\mathrm{1}/\mathrm{2}} \mathrm{3}^{\mathrm{1}/\mathrm{2}} \mathrm{2}} \\ $$$$\frac{{dx}}{{x}^{\mathrm{1}/\mathrm{5}} }=\:\frac{{du}}{\mathrm{2}\sqrt{\mathrm{3}{u}}}\:\centerdot\:\frac{\mathrm{3}^{\mathrm{1}/\mathrm{10}} }{{u}^{\mathrm{1}/\mathrm{10}} }=\:\:\frac{{du}}{\mathrm{2}\centerdot\mathrm{3}^{\mathrm{2}/\mathrm{5}} }\centerdot{u}^{−\mathrm{3}/\mathrm{5}} \:=\frac{{du}}{\mathrm{3}^{\mathrm{2}/\mathrm{5}} }{u}^{\frac{\mathrm{2}}{\mathrm{5}}−\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\:\infty} {x}^{{t}−\mathrm{1}} {e}^{−{x}} {dx}=\Gamma\left({t}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{u}^{\frac{\mathrm{2}}{\mathrm{5}}\:−\mathrm{1}} {e}^{−{u}} {du}=\Gamma\left(\frac{\mathrm{2}}{\mathrm{5}}\right) \\ $$
