Question Number 141419 by mnjuly1970 last updated on 18/May/21
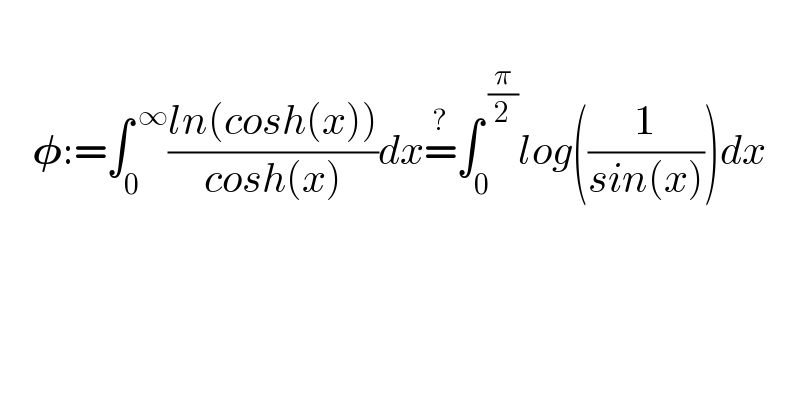
$$ \\ $$$$\:\:\:\:\boldsymbol{\phi}:=\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left({cosh}\left({x}\right)\right)}{{cosh}\left({x}\right)}{dx}\overset{?} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {log}\left(\frac{\mathrm{1}}{{sin}\left({x}\right)}\right){dx} \\ $$
Answered by mindispower last updated on 18/May/21
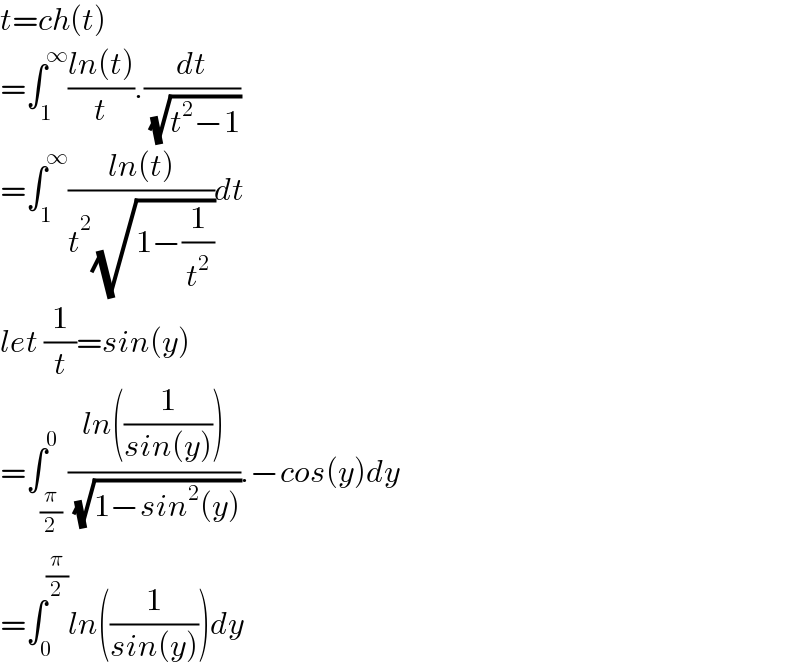
$${t}={ch}\left({t}\right) \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({t}\right)}{{t}}.\frac{{dt}}{\:\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }}}{dt} \\ $$$${let}\:\frac{\mathrm{1}}{{t}}={sin}\left({y}\right) \\ $$$$=\int_{\frac{\pi}{\mathrm{2}}} ^{\mathrm{0}} \frac{{ln}\left(\frac{\mathrm{1}}{{sin}\left({y}\right)}\right)}{\:\sqrt{\mathrm{1}−{sin}^{\mathrm{2}} \left({y}\right)}}.−{cos}\left({y}\right){dy} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\mathrm{1}}{{sin}\left({y}\right)}\right){dy} \\ $$
Commented by mindispower last updated on 18/May/21

$${pleasur} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 18/May/21
$${thanks}\:{alot}\:{sir}\:{power}.. \\ $$
Answered by mnjuly1970 last updated on 18/May/21
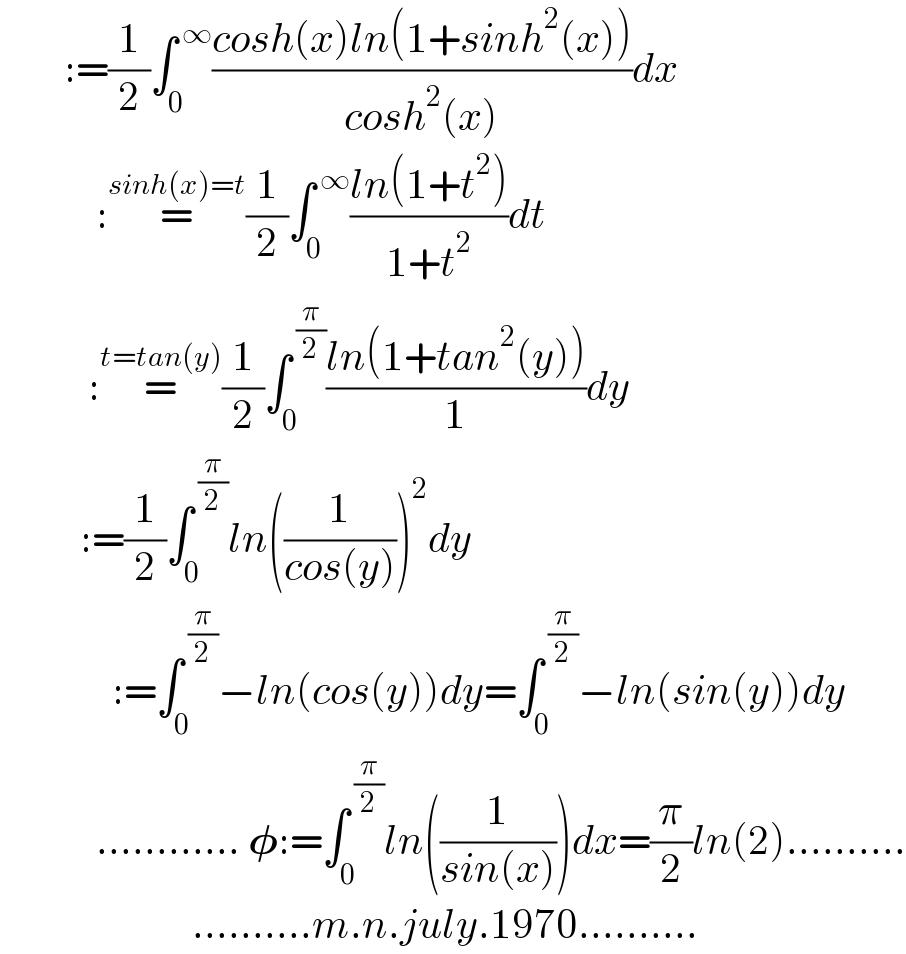
$$\:\:\:\:\:\:\:\::=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{cosh}\left({x}\right){ln}\left(\mathrm{1}+{sinh}^{\mathrm{2}} \left({x}\right)\right)}{{cosh}^{\mathrm{2}} \left({x}\right)}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\::\overset{{sinh}\left({x}\right)={t}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} \frac{{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\:\:\:\:\:\:\:\::\overset{{t}={tan}\left({y}\right)} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \frac{{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left({y}\right)\right)}{\mathrm{1}}{dy} \\ $$$$\:\:\:\:\:\:\:\:\:\::=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\mathrm{1}}{{cos}\left({y}\right)}\right)^{\mathrm{2}} {dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\::=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} −{ln}\left({cos}\left({y}\right)\right){dy}=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} −{ln}\left({sin}\left({y}\right)\right){dy} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:…………\:\boldsymbol{\phi}:=\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} {ln}\left(\frac{\mathrm{1}}{{sin}\left({x}\right)}\right){dx}=\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)………. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:……….{m}.{n}.{july}.\mathrm{1970}………. \\ $$
