Menu Close

0-ln-x-x-2-a-2-5-dx-

Tinku Tara 0 Comments
Pin




Question Number 140388 by benjo_mathlover last updated on 07/May/21
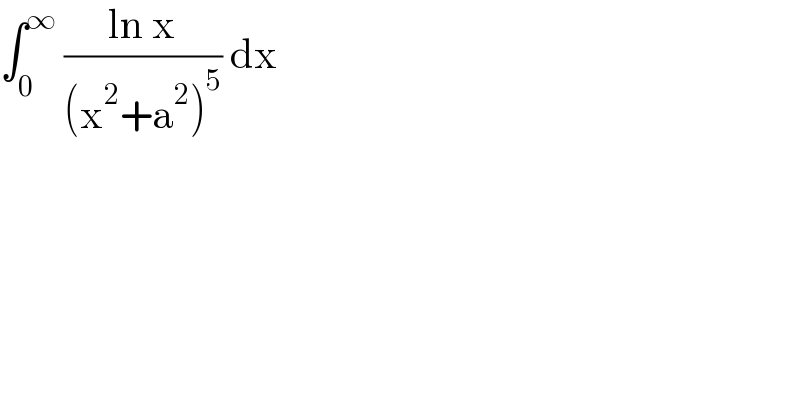
∫_0 ^∞ ((ln x)/((x^2 +a^2 )^5 )) dx
$$\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{ln}\:\mathrm{x}}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{5}} }\:\mathrm{dx}\: \\ $$
Answered by mathmax by abdo last updated on 07/May/21
let f(a)=∫_0 ^∞ ((logx)/((x^2 +a^2 )^4 )) ⇒f^′ (a)=−∫_0 ^∞ ((4(2a)(x^2 +a^2 )^3 )/((x^2 +a^2 )^8 ))logx dx =−8a ∫_0 ^∞ ((logx)/((x^2 +a^2 )^5 )) dx ⇒∫_0 ^∞ ((logx)/((x^2 +a^2 )^5 ))dx =−((f^′ (a))/(8a)) (suppose a>0) cha7gement x=at give f(a)=∫_0 ^∞ ((loga+logt)/(a^8 (t^2 +1)^4 )) adt =((loga)/a^7 )∫_0 ^∞ (dt/((t^2 +1)^4 )) +(1/a^7 )∫_0 ^∞ ((logt)/((t^2 +1)^4 ))dt we have ∫_0 ^∞ (dt/((t^2 +1)^4 )) =(1/2)∫_(−∞) ^(+∞) (dt/((t^2 +1)^4 )) =(1/2)(2iπ)Res(w,i) with w(z)=(1/((z^2 +1)^4 ))=(1/((z−i)^4 (z+i)^4 )) Res(w,i)=lim_(z→i) (1/((4−1)!)){(z−i)^4 w(z)}^((3)) =(1/(3!))lim_(z→i) {(z+i)^(−4) }^((3)) =(1/(3!))lim_(z→i) {−4(z+i)^(−5) }^((2)) =(1/(3!))lim_(z→i) {20 (z+i)^(−6) }^((1)) =(1/(3!))lim_(z→i) (−120)(z+i)^(−7) =−20 (2i)^(−7 ) =((−20)/((2i)^7 )) =−((2^2 ×5)/(2^7 i^7 )) =−i(5/2^5 ) ⇒ ∫_0 ^∞ (dt/((t^2 +1)^4 )) =iπ(−i(5/2^5 )) =((5π)/(32)) and ∫_0 ^∞ ((logt)/((t^2 +1)^4 ))dt =_(t=(√x)) ∫_0 ^∞ ((log((√x)))/((x+1)^4 ))dt =(1/2)∫_0 ^∞ ((logx)/((x+1)^4 ))dx =(1/2)∫_0 ^1 ((logx)/((x+1)^4 ))dx +(1/2)∫_1 ^∞ ((logx)/((x+1)^4 ))dx(→x=(1/y)) =(1/2)∫_0 ^1 ((logx)/((x+1)^4 ))dx−(1/2)∫_0 ^1 ((−logy)/(((1/y)+1)^4 ))(−(dy/y^2 )) =(1/2)∫_0 ^1 ((logx)/((x+1)^4 ))dx−(1/2)∫_0 ^1 ((y^2 logy)/((y+1)^4 ))dy =(1/2)∫_0 ^1 (((1−x^2 )logx)/((x+1)^4 ))dx we ghave (1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n ⇒ −(1/((1+x)^2 )) =Σ_(n=1) ^∞ n(−1)^n x^(n−1) ⇒ ((2(1+x))/((1+x)^4 )) =Σ_(n=2) ^∞ n(n−1)(−1)^n x^(n−2) =(2/((1+x)^3 )) ⇒ ((−2.3(1+x)^2 )/((1+x)^6 )) =Σ_(n=3) ^∞ n(n−1)(n−2)(−1)^n x^(n−3) =−(6/((1+x)^4 )) ⇒ ∫_0 ^1 (((1−x^2 )logx)/((x+1)^4 )) =−(1/6)Σ_(n=3) ^∞ n(n−1)(n−2)(−1)^n ∫_0 ^1 (1−x^2 )x^(n−3) dx =−(1/6) Σ_(n=3) ^∞ n(n−1)(n−2)(−1)^n ∫_0 ^1 (x^(n−3) −x^(n−1) )dx =−(1/6)Σ_(n=3) ^∞ n(n−1)(n−2)(−1)^n [(1/(n−2))x^(n−2) −(1/n)x^n ]_0 ^1 =−(1/6)Σ_(n=3) ^∞ n(n−1)(n−2)(−1)^n ((1/(n−2))−(1/n)) =−(1/6)Σ_(n=3) ^∞ n(n−1)(−1)^n +(1/6)Σ_(n=3) ^∞ (n−1)(n−2)(−1)^n ....be continued....
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{4}} }\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)=−\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{4}\left(\mathrm{2a}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{3}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{8}} }\mathrm{logx}\:\mathrm{dx} \\ $$$$=−\mathrm{8a}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{5}} }\:\mathrm{dx}\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{a}^{\mathrm{2}} \right)^{\mathrm{5}} }\mathrm{dx}\:=−\frac{\mathrm{f}^{'} \left(\mathrm{a}\right)}{\mathrm{8a}}\:\:\left(\mathrm{suppose}\:\mathrm{a}>\mathrm{0}\right) \\ $$$$\mathrm{cha7gement}\:\:\mathrm{x}=\mathrm{at}\:\mathrm{give}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{loga}+\mathrm{logt}}{\mathrm{a}^{\mathrm{8}} \left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:\mathrm{adt} \\ $$$$=\frac{\mathrm{loga}}{\mathrm{a}^{\mathrm{7}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:+\frac{\mathrm{1}}{\mathrm{a}^{\mathrm{7}} }\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{+\infty} \:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{2i}\pi\right)\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)\:\mathrm{with} \\ $$$$\mathrm{w}\left(\mathrm{z}\right)=\frac{\mathrm{1}}{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }=\frac{\mathrm{1}}{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{4}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} } \\ $$$$\mathrm{Res}\left(\mathrm{w},\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\frac{\mathrm{1}}{\left(\mathrm{4}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{4}} \mathrm{w}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{3}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{4}} \right\}^{\left(\mathrm{3}\right)} \:=\frac{\mathrm{1}}{\mathrm{3}!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{−\mathrm{4}\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{5}} \right\}^{\left(\mathrm{2}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\left\{\mathrm{20}\:\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{6}} \right\}^{\left(\mathrm{1}\right)} \:=\frac{\mathrm{1}}{\mathrm{3}!}\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\left(−\mathrm{120}\right)\left(\mathrm{z}+\mathrm{i}\right)^{−\mathrm{7}} \\ $$$$=−\mathrm{20}\:\left(\mathrm{2i}\right)^{−\mathrm{7}\:} \:=\frac{−\mathrm{20}}{\left(\mathrm{2i}\right)^{\mathrm{7}} }\:=−\frac{\mathrm{2}^{\mathrm{2}} ×\mathrm{5}}{\mathrm{2}^{\mathrm{7}} \:\mathrm{i}^{\mathrm{7}} }\:=−\mathrm{i}\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{dt}}{\left(\mathrm{t}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{4}} }\:=\mathrm{i}\pi\left(−\mathrm{i}\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }\right)\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:\:\mathrm{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{logt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dt}\:\:=_{\mathrm{t}=\sqrt{\mathrm{x}}} \:\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}\left(\sqrt{\mathrm{x}}\right)}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}\:+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}\left(\rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{y}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{logy}}{\left(\frac{\mathrm{1}}{\mathrm{y}}+\mathrm{1}\right)^{\mathrm{4}} }\left(−\frac{\mathrm{dy}}{\mathrm{y}^{\mathrm{2}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{y}^{\mathrm{2}} \mathrm{logy}}{\left(\mathrm{y}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dy} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{ghave}\:\frac{\mathrm{1}}{\mathrm{1}+\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{x}\right)}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:=\frac{\mathrm{2}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{3}} }\:\Rightarrow \\ $$$$\frac{−\mathrm{2}.\mathrm{3}\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{6}} }\:=\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}^{\mathrm{n}−\mathrm{3}} \:=−\frac{\mathrm{6}}{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{4}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{logx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{4}} }\:=−\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{n}−\mathrm{3}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\:\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}−\mathrm{3}} −\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left[\frac{\mathrm{1}}{\mathrm{n}−\mathrm{2}}\mathrm{x}^{\mathrm{n}−\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{n}}\mathrm{x}^{\mathrm{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{n}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{n}}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} +\frac{\mathrm{1}}{\mathrm{6}}\sum_{\mathrm{n}=\mathrm{3}} ^{\infty} \left(\mathrm{n}−\mathrm{1}\right)\left(\mathrm{n}−\mathrm{2}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} \\ $$$$….\mathrm{be}\:\mathrm{continued}…. \\ $$
Answered by Dwaipayan Shikari last updated on 07/May/21
ν(ξ)=∫_0 ^∞ (x^ξ /((x^2 +a^2 )^5 ))dx x=au ∫_0 ^∞ ((log(x))/((x^2 +a^2 )^5 ))=ν′(0) ν(ξ)=a^(ξ−9) ∫_0 ^∞ (u^ξ /((u^2 +1)^5 ))dx=(1/2)a^(ξ−9) ∫_0 ^∞ (t^((ξ/2)−(1/2)) /((t+1)^5 ))dt =(a^(ξ−9) /2)∫_0 ^∞ (t^(((ξ+1)/2)−1) /((t+1)^(5+((ξ+1)/2)−((ξ+1)/2)) ))dt=(a^(ξ−9) /2).((Γ(((ξ+1)/2))Γ((9/2)−(ξ/2)))/(Γ(5))) log(ν(ξ))=log((a^(ξ−9) /(48))Γ(((ξ+1)/2))Γ((9/2)−(ξ/2))) ((ν′(ξ))/(ν(ξ)))=log(a)a^(ξ−9) +(1/2)(ψ(((ξ+1)/2))−ψ((9/2)−(ξ/2)) ν′(0)=ν(0)(((log(a))/a^9 )+(1/2)(ψ((1/2))−ψ((1/2))−(2/7)−(2/5)−(2/3)−2)) ν′(0)=(1/(2a^9 ))((((√π).(7/2).(5/2).(3/2).(1/2)(√π))/(4!)))=(π/(768a^9 )) ν′(0)=(π/(768a^9 ))(((log(a))/a^9 )−((12)/(35))−(4/3))=(π/(768a^9 ))(((log(a))/a^9 )−((176)/(105)))
$$\nu\left(\xi\right)=\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\xi} }{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{5}} }{dx}\:\:\:{x}={au} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{log}\left({x}\right)}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{5}} }=\nu'\left(\mathrm{0}\right) \\ $$$$\nu\left(\xi\right)={a}^{\xi−\mathrm{9}} \int_{\mathrm{0}} ^{\infty} \frac{{u}^{\xi} }{\left({u}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{5}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}{a}^{\xi−\mathrm{9}} \int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\xi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}} }{\left({t}+\mathrm{1}\right)^{\mathrm{5}} }{dt} \\ $$$$=\frac{{a}^{\xi−\mathrm{9}} }{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{t}^{\frac{\xi+\mathrm{1}}{\mathrm{2}}−\mathrm{1}} }{\left({t}+\mathrm{1}\right)^{\mathrm{5}+\frac{\xi+\mathrm{1}}{\mathrm{2}}−\frac{\xi+\mathrm{1}}{\mathrm{2}}} }{dt}=\frac{{a}^{\xi−\mathrm{9}} }{\mathrm{2}}.\frac{\Gamma\left(\frac{\xi+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}−\frac{\xi}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{5}\right)} \\ $$$${log}\left(\nu\left(\xi\right)\right)={log}\left(\frac{{a}^{\xi−\mathrm{9}} }{\mathrm{48}}\Gamma\left(\frac{\xi+\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{9}}{\mathrm{2}}−\frac{\xi}{\mathrm{2}}\right)\right) \\ $$$$\frac{\nu'\left(\xi\right)}{\nu\left(\xi\right)}={log}\left({a}\right){a}^{\xi−\mathrm{9}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\xi+\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{9}}{\mathrm{2}}−\frac{\xi}{\mathrm{2}}\right)\right. \\ $$$$\nu'\left(\mathrm{0}\right)=\nu\left(\mathrm{0}\right)\left(\frac{{log}\left({a}\right)}{{a}^{\mathrm{9}} }+\frac{\mathrm{1}}{\mathrm{2}}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\frac{\mathrm{2}}{\mathrm{7}}−\frac{\mathrm{2}}{\mathrm{5}}−\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{2}\right)\right) \\ $$$$\nu'\left(\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{2}{a}^{\mathrm{9}} }\left(\frac{\sqrt{\pi}.\frac{\mathrm{7}}{\mathrm{2}}.\frac{\mathrm{5}}{\mathrm{2}}.\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\pi}}{\mathrm{4}!}\right)=\frac{\pi}{\mathrm{768}{a}^{\mathrm{9}} } \\ $$$$\nu'\left(\mathrm{0}\right)=\frac{\pi}{\mathrm{768}{a}^{\mathrm{9}} }\left(\frac{{log}\left({a}\right)}{{a}^{\mathrm{9}} }−\frac{\mathrm{12}}{\mathrm{35}}−\frac{\mathrm{4}}{\mathrm{3}}\right)=\frac{\pi}{\mathrm{768}{a}^{\mathrm{9}} }\left(\frac{{log}\left({a}\right)}{{a}^{\mathrm{9}} }−\frac{\mathrm{176}}{\mathrm{105}}\right) \\ $$$$ \\ $$
Answered by qaz last updated on 07/May/21
A=∫_0 ^∞ ((lnx)/(x^2 +a^2 ))dx=(1/a)∫_0 ^∞ ((lna+lnx)/(x^2 +1))dx=((πlna)/(2a)) (∂A/∂a)=−2a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^2 ))dx=(π/(2a^2 ))(1−lna) ⇒B=∫_0 ^∞ ((lnx)/((x^2 +a^2 )^2 ))dx=(π/(4a^3 ))(lna−1) (∂B/∂a)=−4a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^3 ))dx=(π/(4a^4 ))(4−3lna) ⇒C=∫_0 ^∞ ((lnx)/((x^2 +a^2 )^3 ))dx=(π/(16a^5 ))(3lna−4) (∂C/∂a)=−6a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^4 ))dx=(π/(16a^6 ))(23−15lna) ⇒D=∫_0 ^∞ ((lnx)/((x^2 +a^2 )^4 ))dx=(π/(96a^7 ))(15lna−23) (∂D/∂a)=−8a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^5 ))dx=(π/(96a^8 ))(176−105lna) ⇒E=∫_0 ^∞ ((lnx)/((x^2 +a^2 )^5 ))dx=(π/(768a^9 ))(105lna−176) (∂E/∂a)=−10a∫_0 ^∞ ((lnx)/((x^2 +a^2 )^6 ))dx=(π/(768a^(10) ))(1689−945lna) ⇒∫_0 ^∞ ((lnx)/((x^2 +a^2 )^6 ))dx=(π/(7680a^(11) ))(945lna−1689) .......
$${A}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{lna}+{lnx}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}=\frac{\pi{lna}}{\mathrm{2}{a}} \\ $$$$\frac{\partial{A}}{\partial{a}}=−\mathrm{2}{a}\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{2}{a}^{\mathrm{2}} }\left(\mathrm{1}−{lna}\right) \\ $$$$\Rightarrow{B}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}=\frac{\pi}{\mathrm{4}{a}^{\mathrm{3}} }\left({lna}−\mathrm{1}\right) \\ $$$$\frac{\partial{B}}{\partial{a}}=−\mathrm{4}{a}\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx}=\frac{\pi}{\mathrm{4}{a}^{\mathrm{4}} }\left(\mathrm{4}−\mathrm{3}{lna}\right) \\ $$$$\Rightarrow{C}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{3}} }{dx}=\frac{\pi}{\mathrm{16}{a}^{\mathrm{5}} }\left(\mathrm{3}{lna}−\mathrm{4}\right) \\ $$$$\frac{\partial{C}}{\partial{a}}=−\mathrm{6}{a}\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{4}} }{dx}=\frac{\pi}{\mathrm{16}{a}^{\mathrm{6}} }\left(\mathrm{23}−\mathrm{15}{lna}\right) \\ $$$$\Rightarrow{D}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{4}} }{dx}=\frac{\pi}{\mathrm{96}{a}^{\mathrm{7}} }\left(\mathrm{15}{lna}−\mathrm{23}\right) \\ $$$$\frac{\partial{D}}{\partial{a}}=−\mathrm{8}{a}\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{5}} }{dx}=\frac{\pi}{\mathrm{96}{a}^{\mathrm{8}} }\left(\mathrm{176}−\mathrm{105}{lna}\right) \\ $$$$\Rightarrow{E}=\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{5}} }{dx}=\frac{\pi}{\mathrm{768}{a}^{\mathrm{9}} }\left(\mathrm{105}{lna}−\mathrm{176}\right) \\ $$$$\frac{\partial{E}}{\partial{a}}=−\mathrm{10}{a}\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{6}} }{dx}=\frac{\pi}{\mathrm{768}{a}^{\mathrm{10}} }\left(\mathrm{1689}−\mathrm{945}{lna}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{lnx}}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{6}} }{dx}=\frac{\pi}{\mathrm{7680}{a}^{\mathrm{11}} }\left(\mathrm{945}{lna}−\mathrm{1689}\right) \\ $$$$……. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *