Question Number 140202 by qaz last updated on 05/May/21
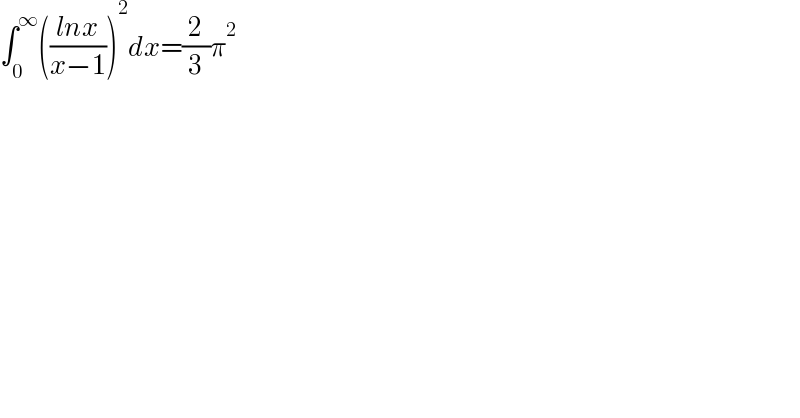
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{lnx}}{{x}−\mathrm{1}}\right)^{\mathrm{2}} {dx}=\frac{\mathrm{2}}{\mathrm{3}}\pi^{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 05/May/21
![Φ =∫_0 ^∞ ((log^2 x)/((1−x)^2 ))dx ⇒Φ=∫_0 ^1 ((log^2 x)/((1−x)^2 ))dx +∫_1 ^∞ ((log^2 x)/((1−x)^2 ))dx(→x=(1/t)) =∫_0 ^1 ((log^2 x)/((1−x)^2 ))dx−∫_0 ^1 ((log^2 t)/((1−(1/t))^2 ))(−(dt/t^2 )) =2∫_0 ^1 ((log^2 x)/((1−x)^2 ))dx we have (1/(1−x)) =Σ_(n=0) ^∞ x^n ⇒(1/((1−x)^2 )) =Σ_(n=1) ^∞ nx^(n−1) (by derivation) ⇒ (1/((1−x)^2 ))=Σ_(n=1) ^∞ nx^(n−1) ⇒Φ =2 ∫_0 ^1 Σ_(n=1) ^∞ nx^(n−1) log^2 x dx =2 Σ_(n=1) ^∞ n U_n with U_n =∫_0 ^1 x^(n−1) log^2 xdx by parts U_n =[(x^n /n)log^2 x]_0 ^1 −∫_0 ^1 (x^n /n)((2logx)/x)dx =−(2/n) ∫_0 ^1 x^(n−1) logx dx =−(2/n)( [(x^n /n)logx]_0 ^1 −∫_0 ^1 (x^n /n)(dx/x)) =−(2/n)(−(1/n) ∫_0 ^1 x^(n−1) dx) =(2/n^3 ) ⇒Φ =2 Σ_(n=1) ^∞ n×(2/n^3 ) =4 Σ_(n=1) ^∞ (1/n^2 ) =4×(π^2 /6) =((2π^2 )/3) ⇒ ∫_0 ^∞ (((logx)/(x−1)))^2 dx =(2/3)π^2](https://www.tinkutara.com/question/Q140231.png)
$$\Phi\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:\:\:\:\Rightarrow\Phi=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:+\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\left(\rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{2}} }\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right)\:=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{we}\:\mathrm{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\:\:\left(\mathrm{by}\:\mathrm{derivation}\right)\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\Phi\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{nx}^{\mathrm{n}−\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\:\mathrm{U}_{\mathrm{n}} \:\:\:\:\mathrm{with}\:\mathrm{U}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\mathrm{log}^{\mathrm{2}} \:\mathrm{xdx}\:\mathrm{by}\:\mathrm{parts} \\ $$$$\mathrm{U}_{\mathrm{n}} =\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{log}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\frac{\mathrm{2logx}}{\mathrm{x}}\mathrm{dx}\:=−\frac{\mathrm{2}}{\mathrm{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{logx}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{n}}\left(\:\left[\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\mathrm{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\frac{\mathrm{dx}}{\mathrm{x}}\right)\:=−\frac{\mathrm{2}}{\mathrm{n}}\left(−\frac{\mathrm{1}}{\mathrm{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \mathrm{dx}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{3}} }\:\Rightarrow\Phi\:=\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}×\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{3}} }\:=\mathrm{4}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\mathrm{4}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{3}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\left(\frac{\mathrm{logx}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{2}} \mathrm{dx}\:=\frac{\mathrm{2}}{\mathrm{3}}\pi^{\mathrm{2}} \\ $$
Answered by Ar Brandon last updated on 05/May/21
![=∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx+∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx=2∫_0 ^1 ((ln^2 x)/((1−x)^2 ))dx =2[−((ln^2 x)/(1−x))+2∫_0 ^1 ((lnx)/(x(1−x)))dx]_0 ^1 =((2ln^2 x)/(x−1))+4∫_0 ^1 [((lnx)/x)+((lnx)/(1−x))]dx =((2ln^2 x)/(x−1))+2ln^2 x+4∫_0 ^1 ((lnx)/(1−x))dx=−4ψ′(1) =4Σ_(n=0) ^∞ (1/((n+1)^2 ))=4ζ(2)=4×(π^2 /6)=((2π^2 )/3)](https://www.tinkutara.com/question/Q140250.png)
$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx}=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }\mathrm{dx} \\ $$$$=\mathrm{2}\left[−\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{1}−\mathrm{x}}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)}\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{2ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}+\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\mathrm{lnx}}{\mathrm{x}}+\frac{\mathrm{lnx}}{\mathrm{1}−\mathrm{x}}\right]\mathrm{dx} \\ $$$$=\frac{\mathrm{2ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}+\mathrm{2ln}^{\mathrm{2}} \mathrm{x}+\mathrm{4}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{lnx}}{\mathrm{1}−\mathrm{x}}\mathrm{dx}=−\mathrm{4}\psi'\left(\mathrm{1}\right) \\ $$$$=\mathrm{4}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{4}\zeta\left(\mathrm{2}\right)=\mathrm{4}×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\mathrm{2}\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$
