Question Number 140200 by qaz last updated on 05/May/21
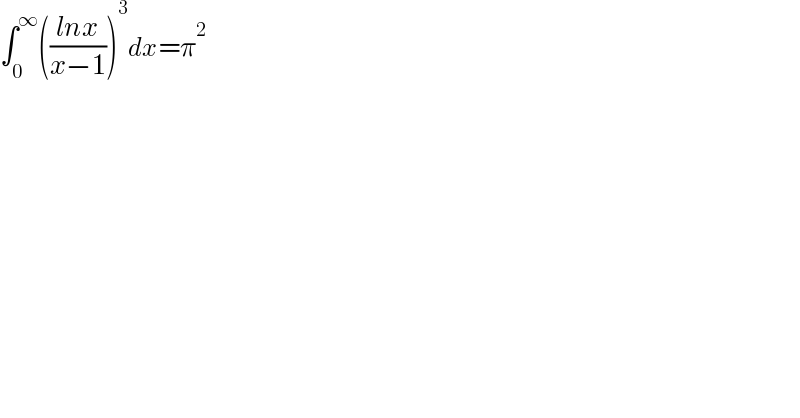
$$\int_{\mathrm{0}} ^{\infty} \left(\frac{{lnx}}{{x}−\mathrm{1}}\right)^{\mathrm{3}} {dx}=\pi^{\mathrm{2}} \\ $$
Commented by Ar Brandon last updated on 05/May/21
![Φ=∫_0 ^∞ (((lnx)/(x−1)))^3 dx=∫_0 ^1 (((lnx)/(x−1)))^3 dx+∫_1 ^∞ (((lnx)/(x−1)))^3 dx =∫_0 ^1 ((ln^3 x)/((x−1)^3 ))dx+∫_0 ^1 ((xln^3 x)/((x−1)^3 ))dx =∫_0 ^1 ((ln^3 x)/((x−1)^2 ))dx+2∫_0 ^1 ((ln^3 x)/((x−1)^3 ))dx =[−((ln^3 x)/(x−1))+3∫((ln^2 x)/(x(x−1)))dx]_0 ^1 +2[−((ln^3 x)/(2(x−1)^2 ))+(3/2)∫((ln^2 x)/(x(x−1)^2 ))dx]_0 ^1 =[−((ln^3 x)/(x−1))−((ln^3 x)/((x−1)^2 ))]_0 ^1 −3[∫((ln^2 x)/x)dx−∫((ln^2 x)/(x−1))dx]_0 ^1 −3[∫((ln^2 x)/(x(x−1)))dx−∫((ln^2 x)/((x−1)^2 ))dx]_0 ^1 =−ln^3 x+3ψ′′(1)+3[∫((ln^2 x)/x)dx−∫((ln^2 x)/(x−1))dx]−3[−((ln^2 x)/(x−1))+2∫((lnx)/(x(x−1)))dx] =−ln^3 x+3ψ′′(1)+ln^3 x−3ψ′′(1)+((3ln^2 x)/(x−1))−6[∫((lnx)/x)dx+∫((lnx)/(x−1))dx] =((3ln^2 x)/(x−1))−3ln^2 x−6ψ′(1)=6Σ_(n=0) ^∞ (1/((n+1)^2 ))=6ζ(2)=π^2](https://www.tinkutara.com/question/Q140251.png)
$$\Phi=\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{lnx}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{3}} \mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{lnx}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{3}} \mathrm{dx}+\int_{\mathrm{1}} ^{\infty} \left(\frac{\mathrm{lnx}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{3}} \mathrm{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xln}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{3}} }\mathrm{dx} \\ $$$$\:\:\:\:=\left[−\frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}+\mathrm{3}\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{2}\left[−\frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{2}}\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=\left[−\frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}−\frac{\mathrm{ln}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{3}\left[\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}}\mathrm{dx}−\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\mathrm{3}\left[\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\mathrm{dx}−\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\:\:\:\:=−\mathrm{ln}^{\mathrm{3}} \mathrm{x}+\mathrm{3}\psi''\left(\mathrm{1}\right)+\mathrm{3}\left[\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}}\mathrm{dx}−\int\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\right]−\mathrm{3}\left[−\frac{\mathrm{ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}+\mathrm{2}\int\frac{\mathrm{lnx}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\mathrm{dx}\right] \\ $$$$\:\:\:\:=−\mathrm{ln}^{\mathrm{3}} \mathrm{x}+\mathrm{3}\psi''\left(\mathrm{1}\right)+\mathrm{ln}^{\mathrm{3}} \mathrm{x}−\mathrm{3}\psi''\left(\mathrm{1}\right)+\frac{\mathrm{3ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}−\mathrm{6}\left[\int\frac{\mathrm{lnx}}{\mathrm{x}}\mathrm{dx}+\int\frac{\mathrm{lnx}}{\mathrm{x}−\mathrm{1}}\mathrm{dx}\right] \\ $$$$\:\:\:\:=\frac{\mathrm{3ln}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}−\mathrm{1}}−\mathrm{3ln}^{\mathrm{2}} \mathrm{x}−\mathrm{6}\psi'\left(\mathrm{1}\right)=\mathrm{6}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{6}\zeta\left(\mathrm{2}\right)=\pi^{\mathrm{2}} \\ $$
Answered by mathmax by abdo last updated on 05/May/21
![I =∫_0 ^∞ ((log^3 x)/((1−x)^3 ))dx ⇒I =−∫_0 ^1 ((log^3 x)/((1−x)^3 ))dx−∫_1 ^∞ ((log^3 x)/((1−x)^3 ))dx(→x=(1/t)) =−∫_0 ^1 ((log^3 x)/((1−x)^3 ))+∫_0 ^1 ((−log^3 t)/((1−(1/t))^3 ))(−(dt/t^2 )) =−∫_0 ^1 ((log^3 x)/((1−x)^3 ))dx−∫_0 ^1 ((tlog^3 t)/((1−t)^3 )) dt =−∫_0 ^1 (((1+x)log^3 x)/((1−x)^3 ))dx we have (1/(1−x))=Σ_(n=0) ^∞ x^n ⇒(1/((1−x)^2 ))=Σ_(n=1) ^∞ nx^(n−1) ⇒((2(1−x))/((1−x)^4 )) =Σ_(n=2) ^∞ n(n−1)x^(n−2) ⇒(2/((1−x)^3 )) =Σ_(n=2) ^∞ n(n−1)x^(n−2) ⇒ I =−(1/2)∫_0 ^1 Σ_(n=2) ^∞ n(n−1)x^(n−2) (1+x)log^3 x dx =−(1/2)Σ_(n=2) ^∞ n(n−1)∫_0 ^1 (x^(n−2) +x^(n−1) )log^3 xdx =−(1/2)Σ_(n=2) ^∞ n(n−1) X_n X_n =∫_0 ^1 (x^(n−2) +x^(n−1) )log^3 xdx =[(x^(n−1) /(n−1))+(x^n /n))log^3 x]_0 ^1 −∫_0 ^1 ((x^(n−1) /(n−1))+(x^n /n))3log^2 x (dx/x) =−3 ∫_0 ^1 ((x^(n−2) /(n−1)) +(x^(n−1) /n))log^2 x dx =−3{ [(x^(n−1) /((n−1)^2 ))+(x^n /n^2 ))log^2 x]_0 ^1 −∫_0 ^1 ((x^(n−1) /((n−1)^2 ))+(x^n /n^2 ))((2logx)/x)dx =6 ∫_0 ^1 ((x^(n−2) /((n−1)^2 )) +(x^(n−1) /n^2 ))log xdx =6{[((x^(n−1) /((n−1)^3 )) +(x^n /n^3 ))logx]_0 ^1 −∫_0 ^1 ((x^(n−1) /((n−1)^3 ))+(x^n /n^3 ))(dx/x) =−6 ∫_0 ^1 ( (x^(n−2) /((n−1)^3 )) +(x^(n−1) /n^3 ))dx =−6[(1/((n−1)^4 ))x^(n−1) +(1/n^4 )x^n ]_0 ^1 =−6((1/((n−1)^4 )) +(1/n^4 )) ⇒ I =3 Σ_(n=2) ^∞ n(n−1)((1/((n−1)^4 ))+(1/n^4 )) =3 Σ_(n=2) ^∞ (n/((n−1)^3 )) +3 Σ_(n=2) ^∞ ((n−1)/n^3 ) =3 Σ_(n=1) ^∞ ((n+1)/n^3 ) +3 Σ_(n=1) ^∞ ((n−1)/n^3 ) =6 Σ_(n=1) ^∞ (1/n^2 ) =6.(π^2 /6)=π^2 ⇒ ∫_0 ^∞ (((logx)/(x−1)))^3 =π^2](https://www.tinkutara.com/question/Q140238.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mathrm{dx}\:\Rightarrow\mathrm{I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mathrm{dx}−\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mathrm{dx}\left(\rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{t}}\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }+\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−\mathrm{log}^{\mathrm{3}} \mathrm{t}}{\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{t}}\right)^{\mathrm{3}} }\left(−\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{tlog}^{\mathrm{3}} \mathrm{t}}{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{3}} }\:\mathrm{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}+\mathrm{x}\right)\mathrm{log}^{\mathrm{3}} \mathrm{x}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \mathrm{nx}^{\mathrm{n}−\mathrm{1}} \\ $$$$\Rightarrow\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{x}\right)}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{4}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}}{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{3}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:\:\Rightarrow \\ $$$$\mathrm{I}\:=−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:\left(\mathrm{1}+\mathrm{x}\right)\mathrm{log}^{\mathrm{3}} \mathrm{x}\:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:+\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\mathrm{log}^{\mathrm{3}} \mathrm{xdx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\:\mathrm{X}_{\mathrm{n}} \\ $$$$\mathrm{X}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:+\mathrm{x}^{\mathrm{n}−\mathrm{1}} \right)\mathrm{log}^{\mathrm{3}} \mathrm{xdx} \\ $$$$\left.=\left[\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}−\mathrm{1}}+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\mathrm{log}^{\mathrm{3}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}−\mathrm{1}}+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\mathrm{3log}^{\mathrm{2}} \mathrm{x}\:\frac{\mathrm{dx}}{\mathrm{x}} \\ $$$$=−\mathrm{3}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{2}} }{\mathrm{n}−\mathrm{1}}\:+\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\right)\mathrm{log}^{\mathrm{2}} \mathrm{x}\:\mathrm{dx} \\ $$$$=−\mathrm{3}\left\{\:\:\left[\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)\mathrm{log}^{\mathrm{2}} \mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\right)\frac{\mathrm{2logx}}{\mathrm{x}}\mathrm{dx} \\ $$$$=\mathrm{6}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{2}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} }\right)\mathrm{log}\:\mathrm{xdx} \\ $$$$=\mathrm{6}\left\{\left[\left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} }\right)\mathrm{logx}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}^{\mathrm{3}} }\right)\frac{\mathrm{dx}}{\mathrm{x}}\right. \\ $$$$=−\mathrm{6}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\:\frac{\mathrm{x}^{\mathrm{n}−\mathrm{2}} }{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{3}} }\:+\frac{\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{3}} }\right)\mathrm{dx}\:=−\mathrm{6}\left[\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{4}} }\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\mathrm{x}^{\mathrm{n}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=−\mathrm{6}\left(\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{4}} }\:+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\right)\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{4}} }\right) \\ $$$$=\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{n}}{\left(\mathrm{n}−\mathrm{1}\right)^{\mathrm{3}} }\:+\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}^{\mathrm{3}} } \\ $$$$=\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}+\mathrm{1}}{\mathrm{n}^{\mathrm{3}} }\:+\mathrm{3}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}−\mathrm{1}}{\mathrm{n}^{\mathrm{3}} } \\ $$$$=\mathrm{6}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\mathrm{6}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\pi^{\mathrm{2}} \:\Rightarrow\:\int_{\mathrm{0}} ^{\infty} \:\left(\frac{\mathrm{logx}}{\mathrm{x}−\mathrm{1}}\right)^{\mathrm{3}} \:=\pi^{\mathrm{2}} \\ $$
