Question Number 3046 by Filup last updated on 03/Dec/15
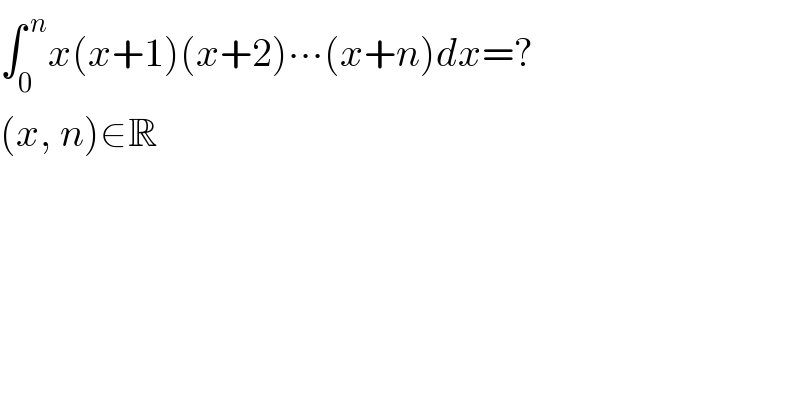
$$\int_{\mathrm{0}} ^{\:{n}} {x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\centerdot\centerdot\centerdot\left({x}+{n}\right){dx}=? \\ $$$$\left({x},\:{n}\right)\in\mathbb{R} \\ $$
Commented by Filup last updated on 04/Dec/15
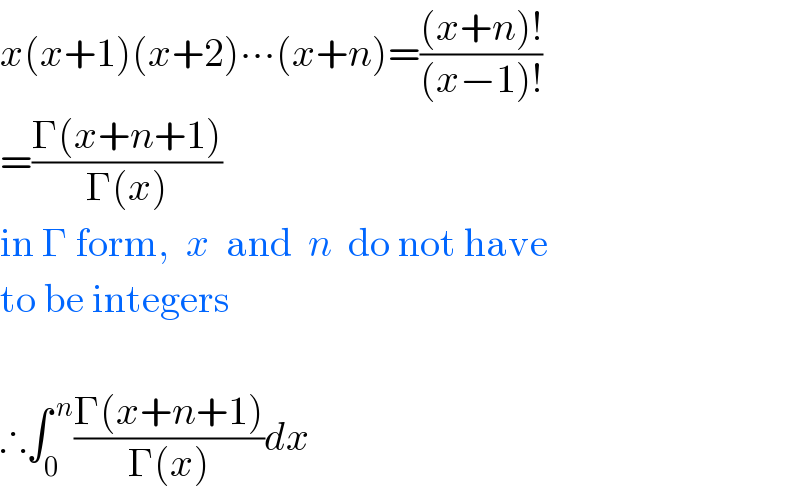
$${x}\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\centerdot\centerdot\centerdot\left({x}+{n}\right)=\frac{\left({x}+{n}\right)!}{\left({x}−\mathrm{1}\right)!} \\ $$$$=\frac{\Gamma\left({x}+{n}+\mathrm{1}\right)}{\Gamma\left({x}\right)} \\ $$$$\mathrm{in}\:\Gamma\:\mathrm{form},\:\:{x}\:\:\mathrm{and}\:\:{n}\:\:\mathrm{do}\:\mathrm{not}\:\mathrm{have} \\ $$$$\mathrm{to}\:\mathrm{be}\:\mathrm{integers} \\ $$$$ \\ $$$$\therefore\int_{\mathrm{0}} ^{\:{n}} \frac{\Gamma\left({x}+{n}+\mathrm{1}\right)}{\Gamma\left({x}\right)}{dx} \\ $$
Commented by prakash jain last updated on 04/Dec/15

$$\mathrm{multiplication}\:\mathrm{and}\:\mathrm{integration}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{done}\:\mathrm{since}\:\mathrm{it}\:\mathrm{is}\:\mathrm{a}\:\mathrm{polynomial}. \\ $$
